Q 1.

In quadrilateral ACBD, AC = AD and AB bisects ∠A (see figure). Show that ∆ABC ≅ ∆ABD. What can you say about BC and BD?

SOLUTION:

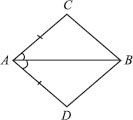
In quadrilateral ACBD, we have AC = AD and AB being the bisector of ∠A.
Now, in ∆ABC and ∆ABD,
AC = AD [Given]
∠CAB = ∠DAB [AB bisects ∠CAD] AB = AB [Common]
∴ ∆ABC ≅ ∆ABD [By SAS congruency]
So, BC = BD [By C.P.C.T.]

Q 2.

ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see figure).
Prove that
(i) ∆ABD≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.

SOLUTION:

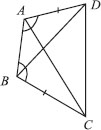
In quadrilateral ABCD, we have
AD = BC and ∠DAB = ∠CBA
In ∆ABD and ∆BAC,
AD = BC [Given]
∠DAB = ∠CBA [Given]
AB = BA [Common]
∴ ∆ABD ≅ ∆BAC [By SAS congruency]

Q 3.

AD and BC are equal perpendiculars to a line segment AB (see figure).
Show that CD bisects AB.

SOLUTION:

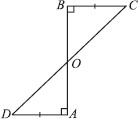
In ∆OBC and ∆OAD, we have
∠OBC = ∠OAD [Each 90°]
BC = AD [Given]
∠BOC = ∠AOD [Vertically opposite angles]
∴ ∆OBC≅ ∆OAD
[By ASA congruency]
⇒ OB = OA [By C.P.C.T.]
i.e., O is the mid-point of AB.
Thus, CD bisects AB.

Q 4.

l and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC≅ ∆CDA.

SOLUTION:

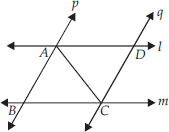
∵ p q and AC is a transversal,
∴ ∠BAC = ∠DCA ...(1)
[Alternate interior angles]
Also l m and AC is a transversal,
∴ ∠BCA = ∠DAC ...(2)
[Alternate interior angles]
Now, in ∆ABC and ∆CDA, we have
∠BAC = ∠DCA [From 1]
CA = AC [Common]
∠BCA = ∠DAC [From 2]
∴ ∆ABC ≅ ∆CDA
[By ASA congruency]

Q 5.

Line l is the bisector of an ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

SOLUTION:

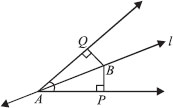
We have, l is the bisector of ∠QAP.
∴ ∠QAB = ∠PAB and
∠Q = ∠P [Each 90°]
⇒ ∠ABQ = ∠ABP
[By angle sum property of ∆]
(i) Now, in ∆APB and ∆AQB, we have
∠ABP = ∠ABQ [Proved above]
AB = AB [Common]
∠PAB = ∠QAB [Given]
∴ ∆APB≅ ∆AQB [By ASA congruency]
(ii) Since∆APB ≅ ∆AQB
⇒ BP = BQ [By C.P.C.T.]
i.e., [Perpendicular distance of B from AP]
= [Perpendicular distance of B from AQ]
Thus, the point B is equidistant from the arms of ∠A.

Q 6.

In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

SOLUTION:

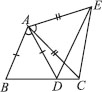
We have ∠BAD = ∠EAC
Adding ∠DAC on both sides, we have ∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠DAE
Now, in ∆ABC and ∆ADE, we have
∠BAC = ∠DAE [Proved]
AB = AD [Given]
AC = AE [Given]
∴ ∆ABC≅ ∆ADE
[By SAS congruency]
⇒ BC = DE. [By C.P.C.T.]

Q 7.

AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE

SOLUTION:

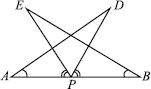
We have, P is the mid-point of AB.
AP = BP
∠EPA = ∠DPB [Given]
Adding ∠EPD on both sides, we get
∠EPA + ∠EPD = ∠DPB + ∠EPD
⇒ ∠APD = ∠BPE
(i) Now, in ∆DAP and ∆EBP, we have
∠PAD = ∠PBE [∠BAD = ∠ABE]
AP = BP [Proved]
∠DPA = ∠EPB [Proved]
∴ ∆DAP≅ ∆ EBP [By ASA congruency]
(ii) Since, ∆DAP≅ ∆EBP
⇒ AD = BE [By C.P.C.T.]

Q 8.

In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such thatDM = CM. Point D is joined to point B (see figure). Show that

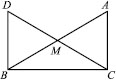
(i) ∆AMC≅ ∆BMD
(ii) ∠DBC is a right angle.
(iii) ∆DBC≅ ∆ACB
(iv)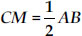

SOLUTION:

Since M is the mid-point of AB. [Given]
∴ BM = AM
(i) In ∆AMC and ∆BMD, we have
CM = DM [Given]
∠AMC = ∠BMD
[Vertically opposite angles]
AM = BM [Proved]
∴ ∆AMC ≅ ∆BMD
[By SAS congruency]
(ii) Since ∆AMC≅ ∆BMD
⇒ ∠MAC = ∠MBD [By C.P.C.T.]
But they form a pair of alternate interior angles.
∴ AC ∥ DB
Now, BC is a transversal which intersects parallel lines AC and DB,
∴ ∠BCA + ∠DBC = 180°
[Co-interior angles]
But ∠BCA = 90°
[∆ABC is right angled at C]
∴ 90° + ∠DBC = 180°
⇒ ∠DBC = 90°
(iii) Again, ∆AMC ≅ ∆BMD [Proved]
∴ AC = BD [By C.P.C.T]
Now, in ∆DBC and ∆ACB, we have
BD = CA [Proved]
∠DBC = ∠ACB [Each 90°]
BC = CB [Common]
∴ ∆DBC ≅ ∆ACB
[By SAS congruency]
(iv) As ∆DBC ≅ ∆ACB
⇒ DC = AB [By C.P.C.T. ]
But DM= CM [Given]

Q 9.

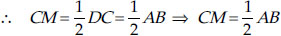
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii)AO bisects ∠A

SOLUTION:

In ∆ABC, we have
AB = AC [Given]
∴ ∠ABC = ∠ACB
[Angles opposite to equal sides of a ∆ are equal]
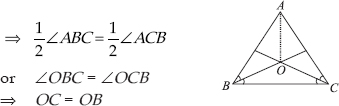
[Sides opposite to equal angles of a ∆ are equal]
(ii) In ∆ABO and ∆ACO, we have
AB = AC [Given]

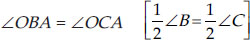
OB = OC [Proved]
∴ ∆ABO ≅ ∆ACO [By SAS congruency]
⇒ ∠OAB = ∠OAC [By C.P.C.T]
⇒ AO bisects ∠A.

Q 10.

In ∆ABC, AD is the perpendicular bisector of BC (see figure). Show that ABC is an isosceles triangle in which AB = AC.

SOLUTION:

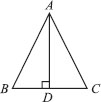
Since AD is bisector of BC.
∴ BD = CD
Now, in ∆ABD and ∆ACD, we have
AD = AD [Common]
∠ADB = ∠ADC = 90°
BD = CD [Proved]
∴ ∆ABD ≅ ∆ACD [By SAS congruency]
⇒ AB = AC [By C.P.C.T]
Thus, ABC is an isosceles triangle.

Q 11.

ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see figure). Show that these altitudes are equal.

SOLUTION:

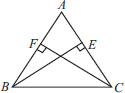
∆ABC is an isosceles triangle.
∴ AB = AC
⇒ ∠ACB = ∠ABC [Angles opposite to equal sides of a ∆ are equal]
⇒ ∠BCE = ∠CBF
Now, in ∆BEC and ∆CFB and we have
∠BCE = ∠CBF [Proved]
∠BEC = ∠CFB [Each 90°]
BC = CB [Common]
∴ ∆BEC ≅ ∆CFB [By AAS congruency]
So, BE = CF [By C.P.C.T]

Q 12.

ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure). Show that
(i) ∆ABE≅ ∆ACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.

SOLUTION:

(i) In ∆ABE and ∆ACF, we have
∠AEB = ∠AFC
[Each 90° as BE ⊥ AC and CF ⊥ AB]
∠A = ∠A [Common]
BE = CF [Given]
∴ ∆ABE ≅ ∆ACF [By AAS congruency]
(ii) Since, ∆ABE ≅ ∆ACF
∴ AB = AC [By C.P.C.T]

Q 13.

ABC and DBC are two isosceles triangles on the same base BC (see figure). Show that ∠ABD = ∠ACD.

SOLUTION:

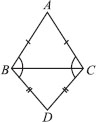
In ∆ABC, we have
AB = AC [ABC is an isosceles triangle]
∴ ∠ABC = ∠ACB ...(1)
[Angles opposite to equal sides of a ∆ are equal]
Again, in ∆BDC, we have
BD = CD [BDC is an isosceles triangle]
∴ ∠CBD = ∠BCD ...(2)
[Angles opposite to equal sides of a ∆ are equal]
Adding (1) and (2), we have
∠ABC + ∠CBD = ∠ACB + ∠BCD
⇒ ∠ABD = ∠ACD.

Q 14.

ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∠BCD is a right angle.

SOLUTION:

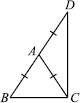
AB = AC [Given] ...(1)
AB = AD [Given] ...(2)
From (1) and (2), we have
AC = AD
Now, in ∆ABC, we have
∠B + ∠ACB + ∠BAC = 180°
[Angle sum property of ∆]
⇒ 2∠ACB + ∠BAC = 180° ...(3)
[∠B = ∠ACB (Angles opposite to equal sides of a ∆ are equal)]
Similarly, In ∆ACD,
∠D + ∠ACD + ∠CAD = 180°
⇒ 2∠ACD + ∠CAD = 180° ...(4)
[∠D = ∠ACD (Angles opposite to equal sides of a ∆ are equal]
Adding (3) and (4), we have
2∠ACB + ∠BAC + 2∠ACD + ∠CAD
= 180° + 180°
⇒ 2[∠ACB + ∠ACD] + [∠BAC + ∠CAD]
= 360°
⇒ 2∠BCD + 180° = 360°
[∠BAC and ∠CAD form a linear pair]
⇒ 2∠BCD = 360° – 180° = 180°

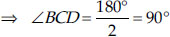
Thus, ∠BCD = 90°

Q 15.

BC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.

SOLUTION:

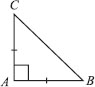
In ∆ABC, we have
AB = AC [Given]
∴ Their opposite angles are equal.
⇒ ∠ACB = ∠ABC
Now, ∠A + ∠B + ∠C = 180°
⇒ 90° + ∠B + ∠C = 180° [∠A = 90°(Given)] ⇒ ∠B + ∠C = 180° – 90°
But ∠ABC = ∠ACB,
i.e., ∠B = ∠C

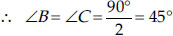
Thus, ∠B = 45° and ∠C = 45°

Q 16.

Show that the angles of an equilateral triangle are 60° each.

SOLUTION:

In ∆ABC, we have

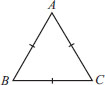
AB = BC = CA
[ABC is an equilateral triangle]
AB = BC ⇒ ∠A = ∠C ...(1)
[Angles opposite to equal sides of a ∆ are equal]
Similarly, AC = BC ⇒ ∠A = ∠B ...(2)
From (1) and (2), we have
∠A = ∠B = ∠C
Let ∠A = ∠B = ∠C = x
Since, ∠A + ∠B + ∠C = 180°
[Angle sum property of ∆]
∴ x + x + x = 180°
⇒ 3x = 180° ⇒ x = 60°
∴ ∠A = ∠B = ∠C = 60°
Thus, the angles of an equilateral triangle are 60° each.

Q 17.

∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that
(i) ∆ABD≅ ∆ACD
(ii) ∆ABP≅ ∆ACP
(iii) AP bisects ∠A
as well as ∠D. (iv) AP is the perpendicular bisector of BC.

SOLUTION:

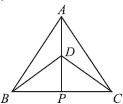
(i) In ∆ABD and ∆ACD, we have
AB = AC [Given]
AD = AD [Common]
BD = CD [Given]
∴ ∆ABD ≅ ∆ACD [By SSS congruency]
⇒ ∠BAD = ∠CAD [By C.P.C.T] ...(1)
(ii) In ∆ABP and ∆ACP, we have
AB = AC [Given]
∠BAP = ∠CAP [Proved] [From (1)]
∴ AP = AP [Common]
∴ ∆ABP ≅ ∆ACP
[By SAS congruency]
(iii) Since, ∆ABP ≅ ∆ACP
⇒ ∠BAP = ∠CAP [By C.P.C.T]
∴ AP is the bisector of ∠A.
Again, in ∆BDP and ∆CDP, we have
BD = CD [Given]
DP = DP [Common]
BP = CP [∵ ∆ABP ≅ ∆ACP]
⇒ ∆BDP ≅ ∆CDP [By SSS congruency]
∴ ∠BDP = ∠CDP [By C.P.C.T]
⇒ DP (or AP) is the bisector of ∠BDC
∴ AP is the bisector of ∠A as well as ∠D.
(iv) As, ∆ABP ≅ ∆ACP
⇒ ∠APB = ∠APC, BP = CP
[By C.P.C.T]
But ∠APB + ∠APC = 180° [Linear Pair]
∴ ∠APB = ∠APC = 90°
⇒ AP ⊥ BC
also BP = CP
Hence, AP is the perpendicular bisector of BC.
Thus, the angles of an equilateral triangle are 60° each.

Q 18.

AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects ∠A

SOLUTION:

(i) In right ∆ABD and ∆ACD, we have
AB = AC [Given]

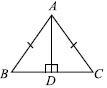
∠ADB = ∠ADC [Each 90°]
AD = AD [Common]
∴ ∆ABD ≅ ∆ACD
[By RHS congruency]
So, BD = CD [By C.P.C.T.]
⇒ D is the mid-point of BC
or AD bisects BC.
(ii) Since, ∆ABD ≅ ∆ACD,
⇒ ∠BAD = ∠CAD [By C.P.C.T.]
So, AD bisects ∠A

Q 19.

Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆PQR (see figure). Show that
(i) ∆ABM ≅ ∆PQN
(ii) ∆ABC ∆PQR

SOLUTION:

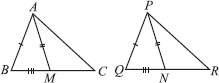
In ∆ABC, AM is the median [Given]

In ∆PQR, PN is the median [Given]

And BC = QR [Given]

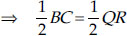
⇒ BM = QN ...(3) [From (1) and (2)]
(i) In ∆ABM and ∆PQN, we have
AB = PQ [Given]
AM = PN [Given]
BM = QN [From (3)] ∴ ∆ABM ≅ ∆PQN [By SSS congruency]
(ii) Since ∆ABM ≅ ∆PQN
⇒ ∠B = ∠Q ...(4) [By C.P.C.T.]
Now, in ∆ABC and ∆PQR, we have
∠B = ∠Q [From (4)]
AB = PQ [Given]
BC = QR [Given]
∴ ∆ABC ≅ ∆PQR [By SAS congruency]

Q 20.

BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

SOLUTION:

Since BE ⊥ AC [Given]
∴ BEC is a right triangle
such that ∠BEC = 90°
Similarly, ∠CFB = 90°

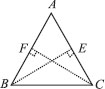
Now, in right ∆BEC and right ∆CFB, we have
BE = CF [Given]
BC = CB [Common]
∠BEC = ∠CFB = 90°
∴ ∆BEC ≅ ∆CFB [By RHS congruency]
So, ∠BCE = ∠CBF [By C.P.C.T.]
or ∠BCA = ∠CBA
Now, in ∆ABC, ∠BCA = ∠CBA
⇒ AB = AC
[Sides opposite to equal angles of a ∆ are equal]
∴ ABC is an isosceles triangle.

Q 21.

ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.

SOLUTION:

We have AP ⊥ BC [Given]
∠APB = 90° and ∠APC = 90°

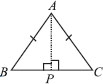
In ∆ABP and ∆ACP, we have
∠APB = ∠APC [Each 90°]
AB = AC [Given]
AP = AP [Common]
∴ ∆ABP ≅ ∆ACP [By RHS congruency]
So, ∠B = ∠C [By C.P.C.T.]

Q 22.

Show that in a right angled triangle, the hypotenuse is the longest side.

SOLUTION:

Let us consider ∆ABC such that ∠B = 90°
∴ ∠A + ∠B + ∠C = 180°
⇒ [∠A + ∠C ] + ∠B = 180° ⇒ ∠A + ∠C = 90° ⇒ ∠A + ∠C = ∠B
∴ ∠B > ∠A and ∠B > ∠C

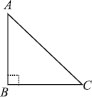
⇒ Side opposite to ∠B is longer than the side opposite to ∠A.
i.e., AC > BC. Similarly, AC > AB.
Therefore, we get AC is the longest side. But AC is the hypotenuse of the triangle.
Thus, hypotenuse is the longest side.

Q 23.

In the given figure, sides AB and AC of ∆ABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

SOLUTION:

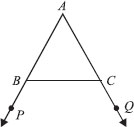
∠ABC + ∠PBC = 180° [Linear pair]
and ∠ACB + ∠QCB = 180° [Linear pair]
But ∠PBC < ∠QCB [Given]
⇒ 180° – ∠PBC > 180° – ∠QCB
⇒ ∠ABC > ∠ACB
⇒ The side opposite to ∠ABC > The side opposite to ∠ACB
⇒ AC > AB.

Q 24.

In the figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

SOLUTION:

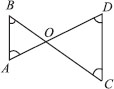
Since ∠B < ∠A [Given]
⇒ ∠A > ∠B
∴ OB > OA ...(1)
[Side opposite to greater angle is longer] Similarly, OC > OD ...(2)
Adding (1) and (2), we have
OB + OC > OA + OD
⇒ BC > AD ⇒ AD < BC.

Q 25.

AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD(see figure). Show that ∠A > ∠ C and ∠B > ∠D.

SOLUTION:

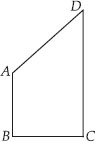
Let us join AC
Now, in ∆ABC, AB < BC
[∴AB is the smallest side of quadrilateral ABCD]
⇒ BC > AB
⇒ ∠BAC > ∠BCA ...(1)
[Angle opposite to longer side of ∆ is larger]

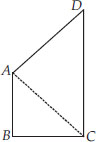
Again, in ∆ACD, CD > AD
[∵ CD is the longest side of the quadrilateral ABCD]
⇒ ∠CAD > ∠ACD ...(2)
[Angle opposite to longer side of ∆ is larger]
Adding (1) and (2), we get
∠BAC + ∠CAD > ∠BCA + ∠ACD
⇒ ∠A > ∠C
Similarly, by joining BD, we have
∠B > ∠D.

Q 26.

In the figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.

SOLUTION:

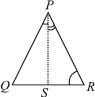
In ∆PQR, PS bisects ∠QPR [Given]
∴ ∠QPS = ∠RPS
and PR > PQ [Given]
⇒ ∠PQS > ∠PRS
[Angle opposite to longer side of ∆ is larger]
⇒ ∠PQS + ∠QPS > ∠PRS + ∠RPS ...(1)
[∠QPS = ∠RPS]
∵ Exterior ∠PSR = [∠PQS + ∠QPS]
and Exterior ∠PSQ = [∠PRS + ∠RPS]
[An exterior angle is equal to the sum of interior opposite angles]
Now, from (1), we have
∠PSR > ∠PSQ.

Q 27.

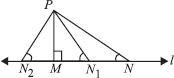
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.

SOLUTION:

Let us consider the
∆PMN such that
∠M = 90°
Since, ∠M + ∠N + ∠P = 180°
[Sum of angles of a triangle]
∵ ∠M = 90° [PM ⊥ l]
So, ∠N + ∠P = ∠M
⇒ ∠N < ∠M
⇒ PM < PN ...(1)
Similarly, PM < PN1 ...(2)
PM < PN2 ...(3)
From (1), (2) and (3), we have PM is the smallest line segment drawn from P on the line l. Thus, the perpendicular segment is the shortest line segment drawn on a line from a point not on it

Q 28.

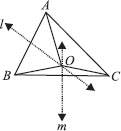
ABC is a triangle. Locate a point in the interior of ∆ABC which is equidistant from all the vertices of ∆ABC.

SOLUTION:

Let us consider a ∆ABC.
Draw l the perpendicular bisector of AB.
Draw m the perpendicular bisector of BC.
Let the two perpendicular bisectors l and m meet at O.
O is the required point which is equidistant from A, B and C.
Note: If we draw a circle with centre O and radius OB or OC, then it will pass through A, B and C. The point O is called circumcentre of the triangle.

Q 29.

In a triangle, locate a point in its interior which is equidistant from all the sides of the triangle.

SOLUTION:

Let us consider a ∆ABC.
Draw l the bisector of ∠B.
Draw m the bisector of ∠C.
Let the two bisectors l and m meet at O.

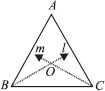
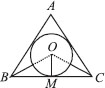
Thus, O is the required point which is equidistant from the sides of ∆ABC.
Note: If we draw OM ⊥ BC and draw a circle with O as centre and OM as radius, then the circle will touch the sides of the triangle.
Point O is called incentre of the triangle.

Q 30.

In a huge park, people are concentrated at three points (see figure):

A : where there are different slides and swings for children.
B : near which a man-made lake is situated.
C : which is near to a large parking and exit.
Where should an ice cream parlour be set up so that maximum number of persons can approach it?
[Hint: The parlour should be equidistant from A, B and C]

SOLUTION:

Let us join A and B, and draw l the perpendicular bisector of AB.
Now, join B and C, and draw m the perpendicular bisector of BC. Let the perpendicular bisectors l and m meet at O. The point O is the required point where the ice cream parlour be set up.
Note: If we join A and C and draw the perpendicular bisectors, then it will also meet (or pass through) the point O.

Q 31.

Complete the hexagonal and star shaped Rangolies [see fig. (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case.
Which has more triangles?

SOLUTION:

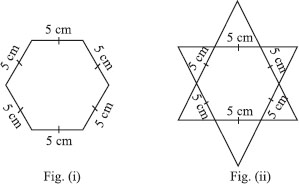
It is an activity. We require 150 equilateral triangles of side 1 cm in the figure (i) and 300 equilateral triangles in the figure (ii).
∴ The figure (ii) has more triangles.