Circles (Mathematics) Class 9 - NCERT Questions
Fill in the blanks:
(i) The centre of a circle pes in _______ of the circle. (exterior/interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius pes in _______ of the circle. (exterior/interior)
(iii) The longest chord of a circle is a _______ of the circle.
(iv) An arc is a _______ when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and _______ of the circle.
(vi) A circle divides the plane, on which it pes, in _______ parts.
(i) interior
(ii) exterior
(iii) diameter
(iv) semicircle
(v) the chord
(vi) three
Write True or False. Give reasons for your answers.
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
(i)True [All points on the circle are equidistant from the centre]
(ii) False [A circle can have an infinite number of equal chords]
(iii) False [Each part will be less than a semicircle]
(iv) True [Diameter = 2 × Radius]
(v) False [The region between the chord and its corresponding arc is a segment]
(vi) True [A circle is drawn on a plane].
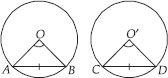
Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
SOLUTION: Given : Two congruent circles with centres O and O' and radii r which have chords AB and CD respectively such that AB = CD.
To Prove : ∠AOB = ∠CO'D
Proof : In ∠AOB and ∠CO'D, we have
AB = CD [Given]
OA = O'C [Each equal to r]
OB = O'D [Each equal to r]
∴ ∆AOB ≅ ∆CO'D [By SSS congruence criteria]
⇒ ∠AOB = ∠CO'D [C.P.C.T.]
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
SOLUTION:Given : Two congruent circles with centres O and O' and radii r which have chords AB and CD respectively such that ∠AOB= ∠CO'D.
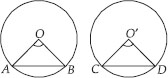
To Prove : AB = CD
Proof : In ∆AOB and ∆CO'D, we have
OA = O'C [Each equal to r]
OB = O'D [Each equal to r]
∠AOB = ∠CO'D [Given]
∴∆AOB ≅ ∆CO'D [By SAS congruence criterion]
Hence, AB = CD [C.P.C.T.].
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
SOLUTION:Let us draw different pairs of circles as shown below:
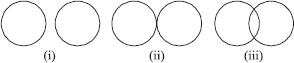
We have

Thus, two circles can have at the most two points in common.
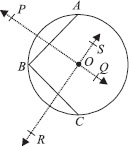
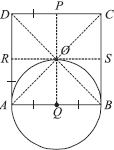
Suppose you are given a circle. Give a construction to find its centre.
SOLUTION: Steps of construction
:
I. Take any three points on the given circle. Let these points be A, B and C.
II. Join AB and BC.
III. Draw the perpendicular bisector PQ of AB.
IV. Draw the perpendicular bisector RS of BC such that it intersects PQ at O.
Thus, 'O' is the required centre of the given circle.
If two circles intersect at two points, prove that their centres pe on the perpendicular bisector of the common chord.
SOLUTION:We have two circles with centres O and O′, intersecting at A and B.
∴ AB is the common chord of two circles and OO′ is the pne segment joining their centres. Let OO′ and AB intersect each other at M.
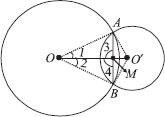
∴ To prove that OO′ is the perpendicular bisector of AB, we join OA, OB, O′A and O′B.
Now, in ∆OAO′ and ∆OBO′, we have
OA = OB [Radii of the same circle]
∴ O′A = O′B [Radii of the same circle]
OO′ = OO′ [Common]
∴ ∆OAO′≅∆OBO′ [By SSS congruence criteria]
⇒ ∠1 = ∠2 [C.P.C.T]
Now, in ∆AOM and ∆BOM, we have
OA = OB [Radii of the same circle]
OM = OM [Common] v
∠1 = ∠2 [Proved above]
∴ ∆AOM ≅∆BOM [SAS criterion]
⇒ ∠3 = ∠4 [C.P.C.T]
But ∠3 + ∠4 = 180° [Linear pair]
∴ ∠3 = ∠4 = 90°
⇒ AM ⊥ OO′
Also AM = BM [C.P.C.T.]
⇒ M is the midpoint of AB.
Thus, OO' is the perpendicular bisector of AB.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
SOLUTION: We have two intersecting circles with centres at O and O′ respectively. Let PQ be the common chord.
∵ In two intersecting circles, the pne joining their centres is perpendicular bisector of the common chord.
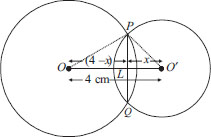
∴ ∠OLP = ∠OLQ = 90° PL = LQ
Now, in right ∆OLP, we have
PL² + OL² = OP² ⇒ PL² + (4 – x)² = 5²
⇒ PL² = 5² – (4 – x)²
⇒ PL² = 25 – 16 – x² + 8x
⇒ PL² = 9 – x² + 8x ...(1)
Again, in ∆O′LP,
PL² = PO′² – LO′² = 3² – x² = 9 – x² ...(2)
From (1) and (2), we have
9 – x² + 8x = 9 – x²
⇒ 8x = 0 ⇒ x = 0
⇒ L and O′ coincide.
∴ PQ is a diameter of the smaller circle.
⇒ PL = 3 cm
But PL = LQ
∴ LQ = 3 cm
∴ PQ = PL + LQ = 3 cm + 3 cm = 6 cm
Thus, the required length of the common chord = 6 cm.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
SOLUTION:Given A circle with centre O. Equal chords AB and CD intersect at E.
To Prove : AE = DE and CE = BE,
Construction : Draw OM ⊥ AB and ON ⊥ CD. Join OE
Proof : Since AB = CD [Given]
∴OM = ON [Equal chords are equidistant from the centre]
Now, in ∆OME and ∆ONE, we have
∠OME = ∠ONE [Each equal to 90° ]
OM = ON [Proved above]
OE = OE [Common]
∴ ∆OME ≅ ∆ONE [By RHS congruence criteria]
⇒ ME = NE [C.P.C.T.]
Adding AM both sides, we get
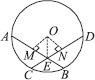
⇒ AM + ME = AM + NE
⇒ AE = DN + NE = DE
[∵ AB = CD ⇒ 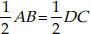
⇒ AM = DN]
⇒ AE = DE ...(1)
Now, AB – AE = CD – DE
⇒ BE = CE ...(2)
From (1) and (2), we have
AE = DE and CE = BE
If two equal chords of a circle intersect within the circle, prove that the pne joining the point of intersection to the centre makes equal angles with the chords.
SOLUTION:Given : A circle with centre O and equal chords AB and CD are intersecting at E.
OE is joined.
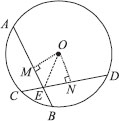
To Prove : ∠OEA = ∠OED
Construction : Draw OM ⊥ AB and ON ⊥ CD.
Proof : In right ∆OME and right ∆ONE,
OM = ON [Equal chords are equidistant
from the centre]
OE = OE [Common]
∠OME = ∠ONE [Each equal to 90° ]
∴ ∆OME ≅ ∆ONE [By RHS congruence]
∴ ∠OEM = ∠OEN [C.P.C.T.]
⇒ ∠OEA = ∠OED
If a pne intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see figure).
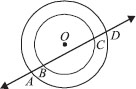
Given : Two circles with the common centre O. A pne ‘l’ intersects the outer circle at A and D and the inner circle at B and C.
To Prove : AB = CD.
Construction : Draw OM ⊥ l.
Proof : For the outer circle.
∵ OM ⊥ l [Construction]
∴ AM = MD ... (1)
[Perpendicular from the centre bisects the chord]
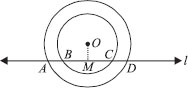
For the inner circle,
∵ OM ⊥ l [Construction]
∴ BM = MC ...(2)
[Perpendicular from the centre to the chord bisects the chord]
Subtracting (2) from (1), we have
AM – BM = MD – MC
⇒ AB = CD
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the
distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Let the three girls Reshma, Salma and Mandip be positioned at R, S and M respectively on the circle of radius 5 m.
RS = SM = 6 m [Given]
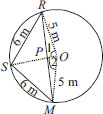
∵ Equal chords of a circle subtend equal angles at the centre.
∴ ∠1 = ∠2 ... (i)
In ∆POR and ∆POM, we have
OP = OP [Common]
OR = OM [Radii of the same circle]
∠1 = ∠2 [Proved above]
∴ ∆POR ≅∆POM [By SAS congruence criteria]
∴ PR = PM and ∠OPR = ∠OPM [C.P.C.T]
∵ ∠OPR + ∠OPM = 180° [Linear pair]
∴ ∠OPR = ∠OPM = 90°
⇒ OP ⊥ RM
Now, in ∆RSP and ∆MSP, we have
RS = MS [6 cm each]
SP = SP [Common]
PR = PM (Proved above)
∴ ∆RSP≅∆MSP [By SSS congruence criteria]
⇒ ∠RPS = ∠MPS [C.P.C.T]
But ∠RPS + ∠MPS = 180°
⇒ ∠RPS = ∠MPS = 90°
∴ SP passes through O.
Let OP = x m
∴ SP = (5 – x) m
Now, in right ∆OPR, we have
x² + RP² = 5² ⇒ RP² = 5² – x² ... (1)
In right ∆SPR, we have
(5 – x)² + RP² = 6²
⇒ RP² = 6² – (5 – x)² ... (2)
From (1) and (2)
∴ 5² – x² = 6² – (5 – x)²
⇒ 2² – x² = 36 – [25 –10x + x²]
⇒ – 10x + 14 = 0 ⇒ 10x = 14
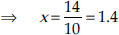
Now, RP² = 5² – x² ⇒ RP² = 25 – (1.4)²
⇒ RP² = 25 – 1.96 = 23.04 m
∴ RP = 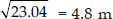
∴ RM = 2RP = 2 × 4.8 m = 9.6 m
Thus, distance between Reshma and Mandip is 9.6 m.
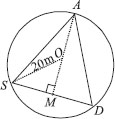
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other.
Find the length of the string of each phone.
Let Ankur, Syed and David are sitting at A, S and D respectively such that AS = SD = AD
i.e. ∆ASD is an equilateral triangle.
Let the length of each side of the equilateral triangle be 2x metres.
Draw AM ⊥ SD.
Since ∆ASD is an equilateral,
∴ AM passes through O.
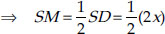
⇒ SM = x
Now, in right ∆ASM, we have
AM² + SM² = AS²
⇒ AM² = AS² – SM² = (2x)² – x²
= 4x² – x² = 3x²
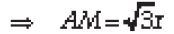
Now, OM = AM – OA = 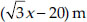
Again, in right ∆OSM, we have
OS² = SM² + OM²
20² = x² + 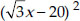
⇒ 400 = x² + 3x² – 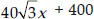
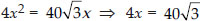
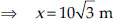
Now, SD = 2x = 2 × 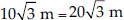
Thus, the length of the string of each phone 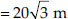
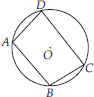
In the given figure A, B and C are three points on a circle with centre O
such that ∠BOC = 30° and ∠AOB = 60°.
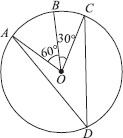
If D is a point on the circle other than the arc ABC, find ∠ADC.
We have a circle with centre O, such that ∠AOB = 60° and ∠BOC = 30°
∵ ∠AOB + ∠BOC = ∠AOC
∴ ∠AOC = 60° + 30° = 90°
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
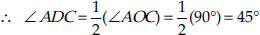
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
SOLUTION:We have a circle having a chord AB equal to radius of the circle.
∴ AO = BO = AB
⇒ ∆AOB is an equilateral triangle.
Since, each angle of an equilateral triangle is 60°.
⇒ ∠AOB = 60°
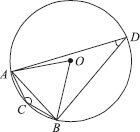
Since, the arc ACB makes reflex ∠AOB = 360° – 60° = 300° at the centre of the circle and ∠ACB at a point on the minor arc of the circle.
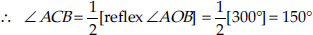
Hence, the angle subtended by the chord on the minor arc = 150°.
Similarly, 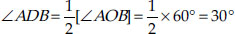
Hence, the angle subtended by the chord on the major arc = 30°
In the given figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
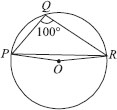
The angle subtended by an arc of a circle at its centre is twice the angle subtended by the same arc at a point on the circumference.
∴ reflex ∠POR = 2∠PQR
But ∠PQR = 100°
∴ reflex ∠POR = 2 × 100° = 200°
Since, ∠POR + reflex ∠POR = 360°
⇒ ∠POR = 360° – 200°
⇒ ∠POR = 160°
Since, OP = OR [Radii of the same circle]
∴ In ∆POR, ∠OPR = ∠ORP
[Angles opposite to equal sides of a triangle are equal]
Also, ∠OPR + ∠ORP + ∠POR = 180°
[Sum of the angles of a triangle is 180°]
⇒ ∠OPR + ∠ORP + 160° = 180°
⇒ 2∠OPR = 180° – 160° = 20°
[∠OPR = ∠ORP]
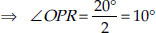
In the given figure, re A, B and C are three points on a circle with centre O
such that ABC = 69°, ∠ACB = 31°, find ∠BDC.
∠ABC + ∠ACB + ∠BAC = 180°
⇒ 69° + 31° + ∠BAC = 180°
⇒ ∠BAC = 180° – 100° = 80°
Since, angles in the same segment are equal.
∴ ∠BDC = ∠BAC ⇒ ∠BDC = 80°
In the figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
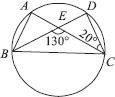
∠BEC = ∠EDC + ∠ECD
[Sum of interior opposite angles is equal to exterior angle]
130° = ∠EDC + 20°
⇒ ∠EDC = 130° – 20° = 110°
⇒ ∠BDC = 110°
Since, angles in the same segment are equal.
∴ ∠BAC = ∠BDC
⇒ ∠BAC = 110°
ABCD is a cycpc quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°,∠BAC = 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
SOLUTION: Since angles in the same segment of a circle are equal.
∴ ∠BAC = ∠BDC
⇒ ∠BDC = 30°
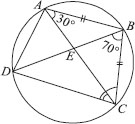
Also ∠DBC = 70° [Given]
∴ In ∆BCD, we have
∠BCD + ∠DBC + ∠CDB = 180°
[Sum of angles of a triangle is 180°]
⇒ ∠BCD + 70° + 30° = 180°
⇒ ∠BCD = 180° – 100° = 80°
Now, in ∆ABC,
AB = BC [Given]
∴ ∠BCA = ∠BAC
[Angles opposite to equal sides of a triangle are equal]
⇒ ∠BCA = 30° [∵ ∠BAC = 30°]
Now, ∠BCA + ∠ECD = ∠BCD
⇒ 30° + ∠ECD = 80°
⇒ ∠ECD = 80° – 30° = 50°
If diagonals of a cycpc quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is rectangle.
Since AC and BD are diameters.
⇒ AC = BD ...(1)
[All diameters of a circle are equal]
Also, ∠BAD = 90° [Angle formed in a semicircle is 90°]
Similarly, ∠ABC = 90°, ∠BCD = 90° and ∠CDA = 90°
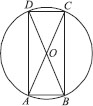
Now, in right ∆ABC and right ∆BAD, we have
AC = BD [From (1)]
AB = BA [Common]
∠ABC = ∠BAD [Each equal to 90°]
∴ ∆ABC ≅ ∆BAD [By RHS congruence criteria]
⇒ BC = AD [C.P.C.T.]
Similarly, AB = DC
Thus, the cycpc quadrilateral ABCD is such that its opposite sides are equal and each of its angle is right angle.
∴ ABCD is a rectangle.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
SOLUTION:We have a trapezium ABCD such thatAB || CD and AD = BC.
Let us draw BE || AD such that ABED is a parallelogram.
∵ The opposite angles of a parallelogram are equal.
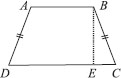
∴ ∠BAD = ∠BED ...(1)
and AD = BE ...(2)
[Opposite sides of a parallelogram]
But AD = BC [Given] ...(3)
∴ From (2) and (3), we have
BE = BC
⇒ ∠BEC = ∠BCE ... (4)
[Angles opposite to equal sides of a triangle are equal]
Now, ∠BED + ∠BEC = 180° [Pnear pair]
⇒ ∠BAD + ∠BCE = 180°
[Using (1) and (4)]
i.e. A pair of opposite angles of quadrilateral ABCD is 180°.
∴ ABCD is cyclic.
⇒ The trapezium ABCD is cyclic.
Two circles intersect at two points B and C. Through B, two pne segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the figure). Prove that ∠ACP = ∠QCD.
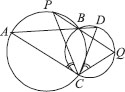
Since angles in the same segment of a circle are equal.
∴ ∠ACP = ∠ABP ...(1)
Similarly, ∠QCD = ∠QBD ...(2)
Since, ∠ABP = ∠QBD [Vertically opposite
angles]
∴ From (1) and (2), we have
∠ACP = ∠QCD
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles pe on the third side.
SOLUTION:We have ∆ABC, and two circles described with diameter as AB and AC respectively. They intersect at a point D, other than A.
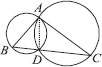
Let us join A and D.
∵ AB is a diameter.
∵ ∠ADB is an angle formed in a semicircle.
⇒ ∠ADB = 90° ...(1)
Similarly, ∠ADC = 90° ...(2)
Adding (1) and (2), we have
∠ADB + ∠ADC = 90° + 90° = 180°
i.e., B, D and C are colpnear points.
⇒ BC is a straight line. Thus, D pes on BC.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that∠CAD = ∠CBD.
SOLUTION:We have ∆ABC and ∆ADC such that they are having AC as their common hypotenuse.
∵ AC is a hypotenuse.
∴ ∠ADC = 90° =∠ABC
∴ Both the triangles are in semi-circle
Case-1 : If both the triangles are in the same semi-circle.
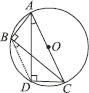
⇒ A, B, C and D are concycpc.
Join BD.
DC is a chord.
∴ ∠CAD and ∠CBD are formed in the same segment.
⇒ ∠CAD = ∠CBD
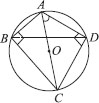
Case-2 : If both the triangles are not in same semi-circle
⇒ A,B,C and D are concycpc. Join BD
DC is a chord
∴ ∠CAD and ∠CBD are formed in the same segment.
⇒ ∠CAD = ∠CBD
Prove that a cyclic parallelogram is a rectangle.
SOLUTION:We have a cycpc parallelogram ABCD. Since, ABCD is a cycpc quadrilateral.
∴ Sum of its opposite angles is 180°
∴ ∠A + ∠C = 180° ...(1)
But ∠A = ∠C ...(2)
[Opposite angles of a parallelogram are equal]
From (1) and (2), we have
∠A = ∠C = 90°
Similarly,
∠B = ∠D = 90°
⇒ Each angle of the parallelogram ABCD is 90°.
Thus, ABCD is a rectangle.
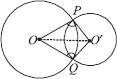
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
SOLUTION: Given : Two circles with centres O and O′ respectively such that they intersect each other at P and Q.
To Prove : ∠OPO′ = ∠OQO′.
Construction : Join OP, O′P, OQ, O′Q and OO′.
Proof : In ∆OPO′ and ∆OQO′, we have
OP = OQ [Radii of the same circle]
O′P = O′Q [Radii of the same circle]
OO′ = OO′ [Common]
∆OPO′ ≅ ∆OQO′ [By SSS congruence criteria]
⇒ ∠OPO′ = ∠OQO′ [C.P.C.T]
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm,
find the radius of the circle. .
We have a circle with centre O. AB || CD and the perpendicular distance between AB and CD is 6 cm and AB = 5 cm, CD = 11 cm.
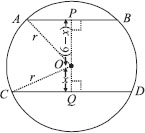
Let ‘r’ be the radius of the circle.
Let us draw OP ⊥ AB and OQ ⊥ CD.
Join OA and OC.
Let OQ = x cm
∴ OP = (6 – x) cm
∵ The perpendicular from the centre of a circle to chord bisects the chord.
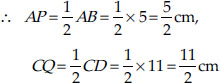
In ∆CQO, we have CO² = CQ² + OQ²
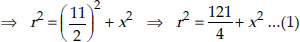
In ∆APO, we have AO² = AP² + OP²
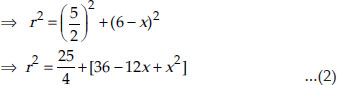
From (1) and (2), we have
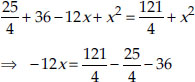
⇒ 12x = 12 ⇒ x = 1
Substituting the value of x in (1), we get
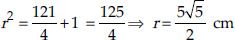
Thus, the radius of the circle is 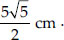
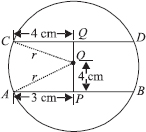
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
SOLUTION:We have a circle with centre O. Parallel chords AB and CD are such that the smaller chord is 4 cm away from the centre.
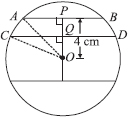
Draw OP ⊥ AB and join OA and OC.
∵ OP ⊥ AB
∴ P is the mid-point of AB.
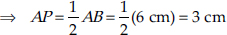
Similarly, 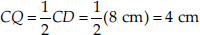
Now in ∆OPA, we have OA² = OP² + AP²
⇒ r² = 4² + 3²
⇒ r² = 16 + 9 = 25
⇒ r = 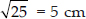 = 5 cm
= 5 cm
[r ≠ –5, because distance cannot be negative]
Again, in ∆CQO, we have OC² = OQ² + CQ²
⇒ r² = OQ² + 4² ⇒ OQ² = r² – 4²
⇒ OQ² = 5² – 4² = 25 – 16 = 9 [∵ r = 5 cm]
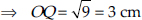
The distance of the other chord (CD) from the centre is 3 cm.
Note: In case we take the two parallel chords on either side of the centre, then
In ∆POA, OA² = OP² + PA² ⇒ r² = 4² + 3² = 5²
⇒ r = 5 cm
In ∆QOC, OC² = CQ² + OQv
⇒ r² = 4² + OQ²
⇒ OQ² = 5² – 4² = 9
⇒ OQ = 3 cm
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the
angles subtended by the chords AC and DE at the centre.
Given : ∠ABC such that when we produce arms BA and BC, they make two equal chords AD and CE. Join AC, DE and AE
Proof : An exterior angle of a triangle is equal to the sum of interior opposite angles.
∴ In ∆BAE, we have
∠DAE = ∠ABC + ∠AEC ...(1)
The chord DE subtends ∠DOE at the centre and ∠DAE in the remaining part of the circle.
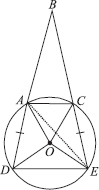
Similarly,
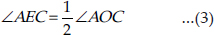
From (1), (2) and (3), we have
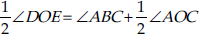
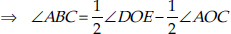
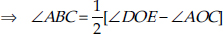
 [(Angle subtended by the chord DE at the centre) – (Angle subtended by the chord AC at the centre)]
[(Angle subtended by the chord DE at the centre) – (Angle subtended by the chord AC at the centre)]
⇒  [Difference of the angles subtended by the chords DE and AC at the centre]
[Difference of the angles subtended by the chords DE and AC at the centre]
Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
SOLUTION:We have a rhombus ABCD such that its diagonals AC and BD intersect at O.
Taking AB as diameter, a circle is drawn. Let us draw PQ || DA and RS || AB, both passing through O. P, Q, R and S are the
mid-points of DC, AB, AD and BC respectively.
All the sides of a rhombus are equal.
AB = DC
⇒ 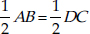
⇒ AQ = DP
⇒ BQ = DP
⇒ AQ = BQ ... (1)
[Q is the midpoint of AB]
Similarly, RA = SB ⇒ RA = OQ ...(2)
[PQ is drawn parallel to AD]
We have, AB = AD [Sides of rhombus]
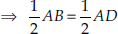
⇒ AR = AQ ... (3)
From (1), (2) and (3), we have QA = QB = QO i.e. A circle drawn with Q as centre, will pass through A, B and O.
Thus, the circle passes through the point of intersection (O) of the diagonals of the rhombus ABCD.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
SOLUTION: Given : A circle passing through A, B and C is drawn such that it intersects CD at E.
ABCE is a cycpc quadrilateral
∴ ∠AEC + ∠B = 180° ...(1)
[Opposite angles of a cycpc quadrilateral are supplementary]
But ABCD is a parallelogram. [Given]
∴ ∠D = ∠B ...(2)
[Opposite angles of a parallelogram are equal]
From (1) and (2), we have
∠AEC + ∠D = 180° ...(3)
But ∠AEC + ∠AED = 180° ...(4)
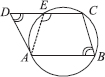
From (3) and (4), we have ∠D = ∠AED
i.e., The base angles of ∆ADE are equal.
∴ Opposite sides must be equal.
⇒ AD = AE
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
SOLUTION:Given : A circle with centre at O. Two chords AC and BD are such that they bisect each other. Let their point of intersection be O.
To Prove : (i) AC and BD are diameters (ii) ABCD is a rectangle
Construction : Join AB, BC, CD and DA.
Proof :
(i) In ∆AOB and ∆COD, we have
AO = CO [O is the mid-point of AC]
BO = DO [O is the mid-point of BD]
∠AOB = ∠COD [Vertically opposite angles]
∴ Using the SAS criterion of congruence,
∆AOB ≅ ∆COD
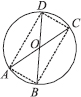
⇒ AB = CD [C.P.C.T.]
⇒ arc AB = arc CD ...(1)
Similarly,
arc AD = arc BC ...(2)
Adding (1) and (2), we get
arc AB + arc AD = arc CD + arc BC
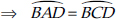
⇒ BD divides the circle into two equal parts.
∴ BD is a diameter.
Similarly, AC is a diameter.
(ii) We know that ∆AOB ≅ ∆COD
⇒ ∠OAB = ∠OCD [C.P.C.T]
⇒ ∠CAB = ∠ACD
⇒ AB || DC
Similarly, AD || BC
∴ ABCD is a parallelogram
Since, opposite angles of a parallelogram are equal
∴ ∠DAB = ∠DCB
But ∠DAB + ∠DCB = 180°
[Sum of the opposite angles of a cycpc quadrilateral is 180°]
⇒ ∠DAB = 90° = ∠DCB
Thus, ABCD is a rectangle.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are
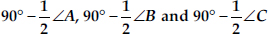
Given : A triangle ABC inscribed in a circle, such that bisectors of ∠A, ∠B and ∠C intersect the circumcircle at D, E and F respectively.
Construction : Join DE, EF and FD.
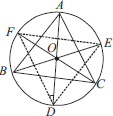
Proof : Angles in the same segment are equal.
∴ ∠FDA = ∠FCA ...(1)
∠EDA = ∠EBA ...(2)
Adding (1) and (2), we have
∠FDA + ∠EDA = ∠FCA + ∠EBA
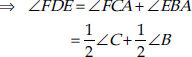
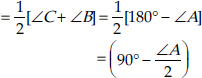
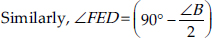
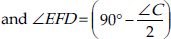
Thus, the angles of ∆DEF are
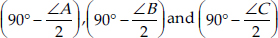
Two congruent circles intersect each other at points A and B. Through A any pne segment PAQ is drawn so that P, Q pe on the two circles. Prove that BP = BQ.
SOLUTION:We have two congruent circles such that they intersect each other at A and B. A pne passing through A, meets the
circles at P and Q. Let us draw the common chord AB.
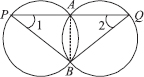
Since angles subtended by equal chords in the congruent circles are equal.
⇒ ∠APB = ∠AQB
Now, in ∆PBQ, we have
∠APB = ∠AQB
So, their opposite sides must be equal.
⇒ PB = BQ.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
SOLUTION:∆ABC with O as centre of its circumcircle. The perpendicular bisector of BC passes through O.
Suppose it cut circumcircle at P.
In order to prove that the perpendicular bisector of BC and bisector of angle A of ∆ABC intersect at P, it is sufficient to
show that AP is bisector of ∠A of ∆ABC.
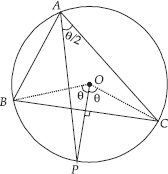
Arc BC makes angle Θ on the circumference
∴ ∠BOC = 2Θ
[Angle at centre is double the angle made by an arc at circumference]
Also, in ∆BOC, OB = OC and OP is perpendicular bisector of BC.
So, ∠BOP = ∠COP = Θ
Arc CP makes angle Θ at O, so it will make angle
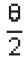 at circumference.
at circumference.
So, ∠CAP = 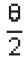
Hence, AP is angle bisector of ∠A of ∆ABC.