Triangles and Properties (Maths) Class 7 - NCERT Questions
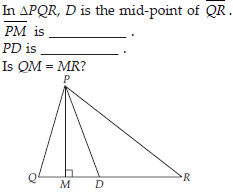
(i) PM is an Altitude
(ii) PD is a Median (iii) No, QM ≠ MR.
Draw rough sketches for the following:
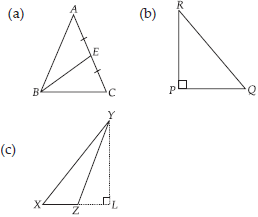
(A) In ∆ABC, BE is a median.
(B) In ∆PQR, PQ and PR are altitudes of the triangle.
(C) In ∆XYZ, YL is an altitude in the exterior of the triangle.
Verify by drawing a diagram, if the median and altitude of an isosceles triangle can be same.
SOLUTION: 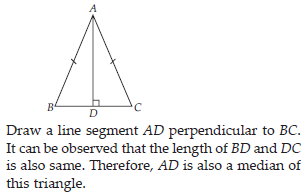
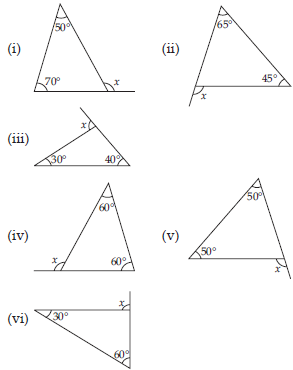
Find the value of the unknown exterior angle x in the following diagrams:

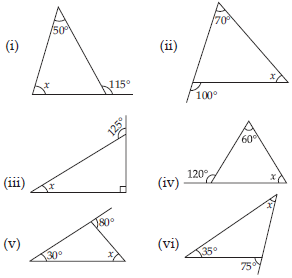
Find the value of the unknown interior angle x in the following figures:

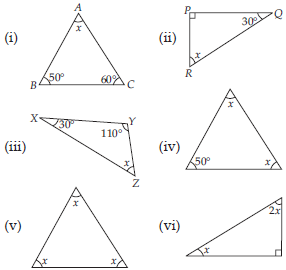
Find the value of the unknown x in the following diagrams:

Find the values of the unknowns x and y in the following diagrams:


Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm
(ii) 3 cm, 6 cm, 7 cm
(iii) 6 cm, 3 cm, 2 cm
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
(i) Given that, the sides of the triangle are
2 cm, 3 cm, 5 cm.
It can be observed that,
2 + 3 = 5 cm
However, 5 cm = 5 cm
Hence, this triangle is not possible.
(ii) Given that, the sides of the triangle are
3 cm, 6 cm, 7 cm.
Here, 3 + 6 = 9 cm > 7 cm
6 + 7 = 13 cm > 3 cm
3 + 7 = 10 cm > 6 cm
Hence, this triangle is possible.
(iii) Given that, the sides of the triangle are
6 cm, 3 cm, 2 cm.
Here, 6 + 3 = 9 cm > 2 cm
However, 3 + 2 = 5 cm < 6 cm
Hence, this triangle is not possible.
Take any point O in the interior of a triangle PQR. Is
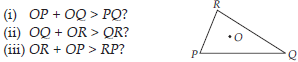
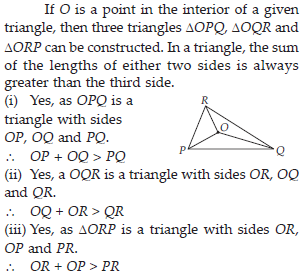
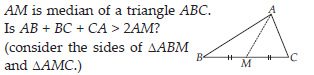
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
In DABM,
AB + BM > AM ...(i)
Similarly, in DACM,
AC + CM > AM ...(ii)
Adding (i) and (ii)
AB + BM + MC + AC > AM + AM
AB + BC + AC > 2AM
Yes, the given expression is true.
ABCD is a quadrilateral.
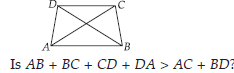

ABCD is a quadrilateral. Is AB + BC + CD + DA < 2(AC + BD)?
SOLUTION: 
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
SOLUTION:Lengths of two sides of a triangle are 12 cm and 15 cm.
In a triangle, the sum of the lengths of either two side is always greater than the third side.
Let the side be x.
∴ x + 12 > 15 ⇒ x > 3
x + 15 > 12 ⇒ x > – 3 but side length never
be –ve.
and 12 + 15 > x ⇒ 27 > x
Hence, third side can measure between
3 and 27.
PQR is a triangle, right-angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
SOLUTION: 
ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
SOLUTION: 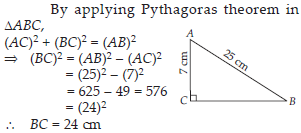
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
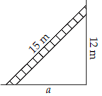
By applying Pythagoras theorem,
(15)2 = (12)2 + a2
⇒ 225 = 144 + a2
⇒ a2 = 225 – 144 = 81 = 92
⇒ a = 9 m
Therefore, the distance of the foot of the ladder from the wall is 9 m.
Which of the following can be the sides of a right triangle?
(i) 2.5 cm, 6.5 cm, 6 cm
(ii) 2 cm, 2 cm, 5 cm
(iii) 1.5 cm, 2 cm, 2.5 cm
In the case of right-angled triangles, identify the right angles.
(i) 2.5 cm, 6.5 cm, 6 cm
∴ (2.5)2 = 6.25, (6.5)2 = 42.25 and (6)2 = 36
It can be observed that,
36 + 6.25 = 42.25
⇒ (6)2 + (2.5)2 = (6.5)2
The square of the length of one side is the sum of the squares of the lengths of the remaining two sides. Hence, these are the sides of a right-angled triangle. Right angle will be in front of the side of measure 6.5 cm.
(ii) 2 cm, 2 cm, 5 cm
∴ (2)2 = 4, (2)2 = 4 and (5)2 = 25
Here, (2)2 + (2)2 ≠ (5)2
The square of the length of one side is not equal to the sum of the square of the lengths of the remaining two sides. Hence, these sides are not of a right-angled triangle.
(iii) 1.5 cm, 2 cm, 2.5 cm
∴ (1.5)2 = 2.25, (2)2 = 4 and (2.5)2 = 6.25
Here, 2.25 + 4 = 6.25
⇒ (1.5)2 + (2)2 = (2.5)2
The square of the length of one side is the sum of the squares of the lengths of the remaining two sides. Hence, these are the sides of a right-angled triangle.
Right angle will be in front of the side of
measure 2.5 cm.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
SOLUTION:In the given figure, BC represents the unbroken part of the tree. Point C represents the point where the tree broke and CA represents the broken part of the tree. Triangle ABC, thus formed, is right-angled at B.

Angles Q and R of a ∆PQR are 25° and 65°.
Write which of the following is true:
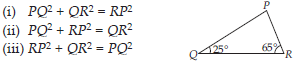
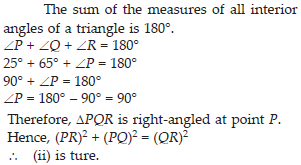
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
SOLUTION: 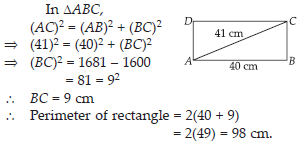
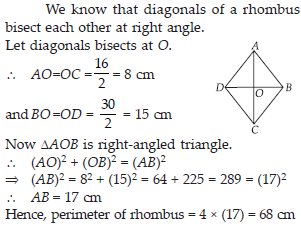
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
SOLUTION: