Symmetry (Mathematics) Class 6 - NCERT Questions
List any four symmetrical objects from your home or school.
SOLUTION:Notebook, Blackboard, Glass, Inkpot.
Q 2. For the given figure, which one is the mirror line, l1 or l2?
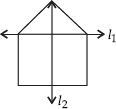
l2 is the mirror line as both sides of the line l2 are symmetric.
Q 3. Identify the shapes given below. Check whether they are symmetric or not. Draw the line of symmetry as well.
(A) 
(B) 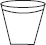
(C) 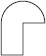
(D) 
(E) 
(F) 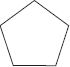
(A) Symmetric
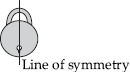
(B) Symmetric
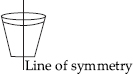
(C) Not symmetric
(D) Symmetric

(E) Symmetric
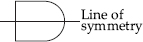
(F) Symmetric
Copy the following on a squared paper. A square paper is what you would have used in your arithmetic notebook in earlier classes. Then complete them such that the dotted line is the line of symmetry.
(A) 
(B) 
(C) 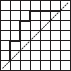
(D) 
(E) 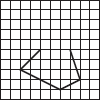
(F) 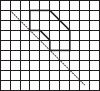
(A) 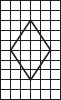
(B) 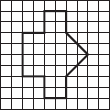
(C) 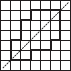
(D) 
(E) 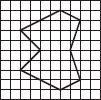
(F) 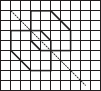
In the figure, l is the line of symmetry. Complete the diagram to make it symmetric.
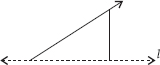
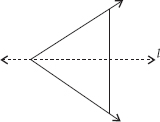
In the figure, l is the line of symmetry. Draw the image of the triangle and complete the diagram so that it becomes symmetric.
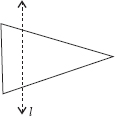
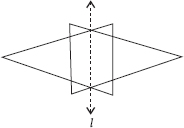
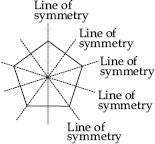
Find the number of lines of symmety for each of the following shapes :
(A) 
(B) 
(C) 
(D) 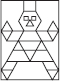
(E) 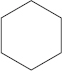
(F) 
(G) 
(H) 
(I) 
(A) 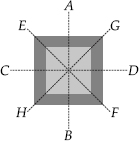
Lines of symmetry are AB, CD, EF and GH.
∴ Number of lines of symmetry = 4
(B) 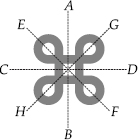
Lines of symmetry are AB, CD, EF and GH.
∴ Number of lines of symmetry = 4
(C) 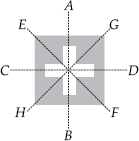
Lines of symmetry are AB, CD, EF and GH.
∴ Number of lines of symmetry = 4
(D) 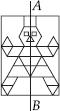
Line of symmetry is AB.
∴ Number of lines of symmetry = 1
(E) 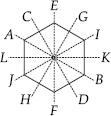
Lines of symmetry are AB, CD, EF, GH, IJ and KL.
∴ Number of lines of symmetry = 6
(F) 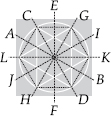
Lines of symmetry are AB, CD, EF, GH, IJ and KL.
∴ Number of lines of symmetry = 6
(G) No line of symmetry.
(H) No line of symmetry.
(I) 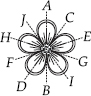
Lines of symmetry are AB, CD, EF, GH and IJ.
∴ Number of lines of symmetry = 5
Copy the triangle in each of the following figures on squared paper. In each case, draw the line(s) of symmetry, if any and identify the type of triangle. (Some of you may like to trace the figures and try paper-folding first!)
(A) 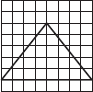
(B) 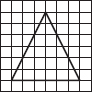
(C) 
(D) 
(A) 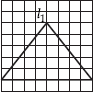
l1 is the line of symmetry.
Isosceles triangle.
(B) 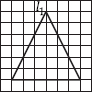
l1 is the line of symmetry.
Isosceles triangle.
(C) 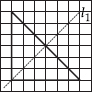
l1 is the line of symmetry.
Isosceles right angled triangle.
(D) 
No line of symmetry.
Scalene triangle.
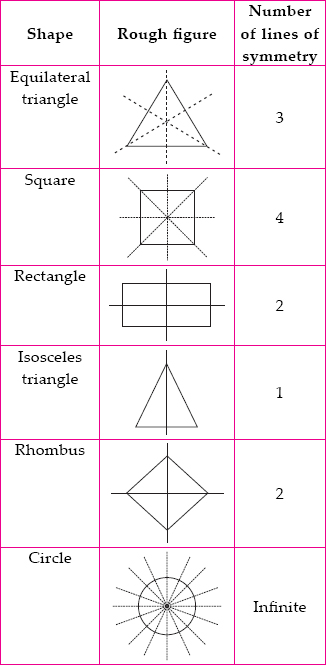
Complete the following table.
Can you draw a triangle which has
(A) exactly one line of symmetry?
(B) exactly two lines of symmetry?
(C) exactly three lines of symmetry?
(D) no lines of symmetry?
Sketch a rough figure in each case.
(A) Yes, isosceles triangle has exactly one line of symmetry.
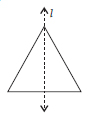
(B) No triangle can be formed which has exactly two lines of symmetry.
(C) Yes, equilateral triangle has three lines of symmetry.
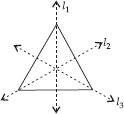
(D) Yes, scalene triangle has no line of symmetry.
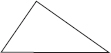
On a squared paper, sketch the following:
(A) A triangle with a horizontal line of symmetry but no vertical line of symmetry.
(B) A quadrilateral with both horizontal and vertical lines of symmetry.
(C) A quadrilateral with a horizontal line of symmetry but no vertical line of symmetry.
(D) A hexagon with exactly two lines of symmetry.
(E) A hexagon with six lines of symmetry.
(Hint : It will be helpful if you first draw the lines of symmetry and then complete the figures.)
(A) 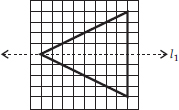
(B) 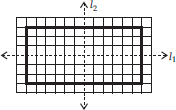
(C) 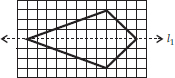
(D) 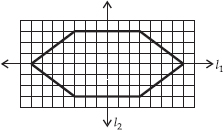
(E) 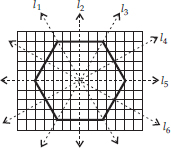
Trace each figure and draw the lines of symmetry, if any:
(A) 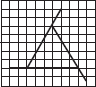
(B) 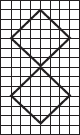
(C) 
(D) 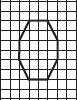
(E) 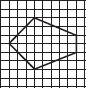
(F) 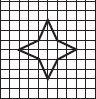
(A) No line of symmetry
(B) 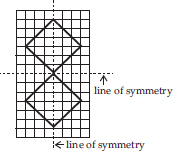
(C) 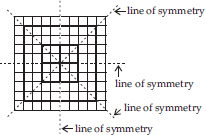
(D) 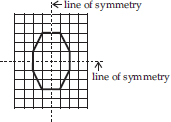
(E) 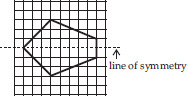
(F) 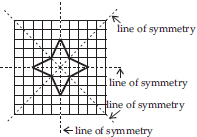
Consider the letters of English alphabets, A to Z. List among them the letters which have
(A) vertical lines of symmetry (like A)
(B) horizontal lines of symmetry (like B)
(C) no lines of symmetry (like Q)
(A) The letters which have vertical lines of symmetry are A, H, I, M, O, T, U, V, W, X, Y.
(B) The letters which have horizontal lines of symmetry are B, C, D, E, H, I, K, O, X.
(C) The letters which have no line of symmetry are F, G, J, L, N, P, Q, R, S, Z
Given here are figures of a few folded sheets and designs drawn about the fold. In each case, draw a rough diagram of the complete figure that would be seen when the design is cut off.
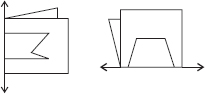
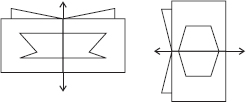
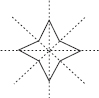
Find the number of lines of symmetry in each of the following shapes. How will you check your answers?
(A) 
(B) 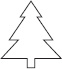
(C) 
(D) 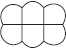
(E) 
(F) 
(A) Number of lines of symmetry = 4
(B) Number of lines of symmetry = 1
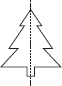
(C) Number of lines of symmetry = 2
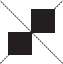
(D) Number of lines of symmetry = 2
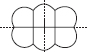
(E) Number of lines of symmetry = 1
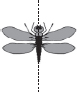
(F) Number of lines of symmetry = 2
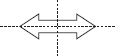
Copy the following drawing on squared paper. Complete each one of them such that the resulting figure has two dotted lines as two lines of symmetry.
(A) 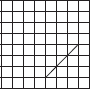
(B) 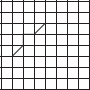
(C) 
(D) 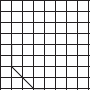
(E) 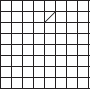
(F) 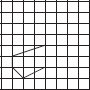
(A) 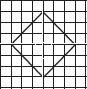
(B) 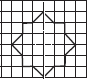
(C) 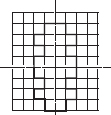
(D) 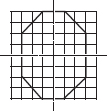
(E) 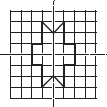
(F) 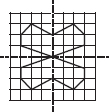
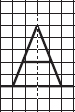
In each figure alongside, a letter of the alphabet is shown along with a vertical line. Take the mirror image of the letter in the given line. Find which letters look the same after reflection (i.e. which letters look the same in the image) and which do not. Can you guess why?
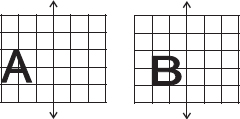
Try for 
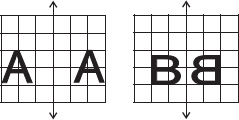
∴ The letter A will look same after reflection.
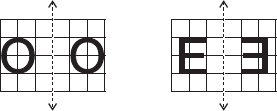
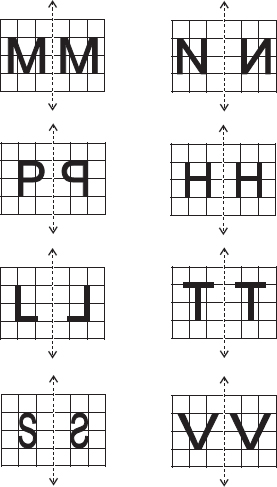
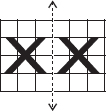
Letters which look same after reflection are A, O, M, H, T, V, X and which do not look same after reflection are B, E, N, P, L, S.