Q 1.

The graphs of y = p(x) are given in the below figures, for some polynomials p(x ). Find the number of zeroes of p(x), in each case.

SOLUTION:

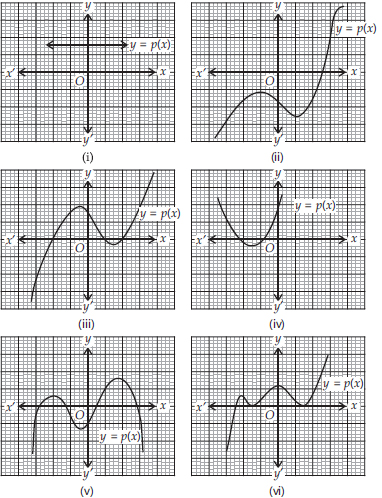
Soln. : (i) The given graph is parallel to x-axis, it does not intersect the x-axis.
∴ It has no zero.
(ii) The given graph intersects the x-axis at one point only.
∴ It has one zero.
(iii) The given graph intersects the x-axis at three points.
∴ It has three zeroes.
(iv) The given graph intersects the x-axis at two points.
∴ It has two zeroes.
(v) The given graph intersects the x-axis at four points.
∴ It has four zeroes.
(vi) The given graph meets the x-axis at three points.
∴ It has three zeroes.

Q 2.

Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x² - 2 x - 8
(ii) 4s² - 4s + 1
(iii) 6x² - 3 - 7x
(iv) 4u² + 8u
(v) t² - 15
(vi) 3x² - x - 4

SOLUTION:

Soln. : (i) We have p(x) = x² - 2x - 8
= x² + 2x - 4x - 8
= x(x + 2) - 4(x + 2)
= (x - 4)(x + 2)
For p(x) = 0, we have (x - 4)(x + 2) = 0
Either x - 4 = 0 ⇒ x = 4 or x + 2 = 0 ⇒ x = - 2
∴ The zeroes of x² - 2x - 8 are 4 and - 2
Now, sum of the zeroes =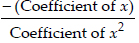

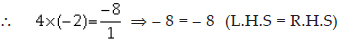
Thus, the relationship between zeroes and the coefficients in x² - 2x - 8 is verified.
(ii)We have p(s) = 4s² - 4s + 1
= 4s² - 2s - 2s + 1
= 2s(2s - 1) - 1(2s - 1)
= (2s - 1)(2s - 1)

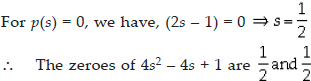
Sum of the zeroes
Sum of the zeroes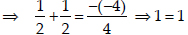
Sum of the zeroes
Sum of the zeroes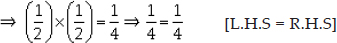
Thus, the relationship between the zeroes and coefficients in the polynomial 4s² - 4s + 1 is verified.
(iii)We have p(x) = 6x² - 3 - 7x
= 6x² - 7x - 3
= 6x² - 9x + 2x - 3
= 3x(2x - 3) + 1(2x - 3)
= (3x + 1)(2x - 3)
For p(x) = 0, we have,

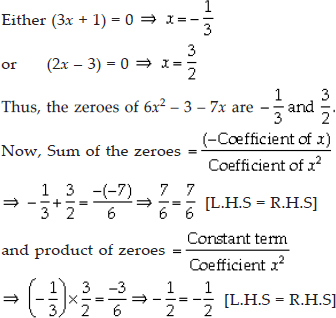
Thus, the relationship between the zeroes and coefficients in the polynomial 6x² - 3 - 7x is verified.
(iv)We have, f(u) = 4u² + 8u = 4u(u + 2)
For f(u) = 0,
Either4u = 0 ⇒ u = 0
or u + 2 = 0 ⇒ u = -2
∴ The zeroes of 4u² + 8u are 0 and - 2.
Now, 4u² + 8u can be written as 4u² + 8u + 0.

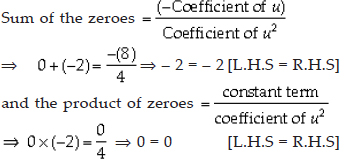
Thus, the relationship between zeroes and the coefficients in the polynomial 4u² + 8u is verified.
(v)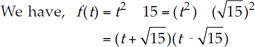
For f(t) = 0, we have

Thus, the relationship between zeroes and the coefficients in the polynomial t² - 15 is verified.
(vi) We have, f(x) = 3x² - x - 4
= 3x² + 3x - 4x - 4
= 3x(x + 1) - 4(x + 1)
= (x + 1)(3x - 4)
For f(x) = 0 ⇒ (x + 1)(3x - 4) = 0
Either(x + 1) = 0 ⇒ x = -1

Thus, the relationship between the zeroes and coefficients in 3x² - x - 4 is verified

Q 3.

Find a quadratic polynomial each with the given numbers as sum and product of its zeroes respectively.
(i)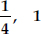
(ii)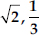
(iii)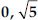
(iv) 1, 1
(v)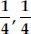
(vi) 4, 1

SOLUTION:

Soln. : (i) Since, sum of the zeroes,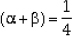
Product of the zeroes, αβ = - 1
∴ The required quadratic polynomial is
x² - (α + β)x + αβ
=
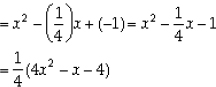
Since, 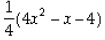and (4x² - x - 4) have same zeroes, therefore (4x² - x - 4) is the required quadratic polynomial.
(ii) Since, sum of the zeroes,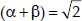
Product of zeroes,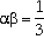
∴ The required quadratic polynomial is
x² - (α + β)x + αβ


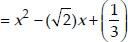
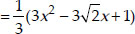
Since, 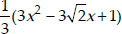and 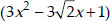have same zeroes, therefore 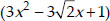is the required quadratic polynomial.
(iii) Since, sum of zeroes, (α + β) = 0
Product of zeroes,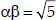
∴ The required quadratic polynomial is
x² - (α + β)x + αβ

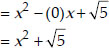
(iv) Since, sum of zeroes, (α + β) = 1
Product of zeroes, αβ = 1
∴ The required quadratic polynomial is
x² - (α + β)x + αβ
= x² - (1)x + 1 = x² - x + 1
(v) Since, sum of the zeroes, 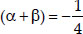Product of zeroes,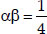
∴ The required quadratic polynomial is
x² - (α + β)x + αβ


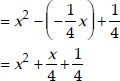
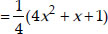
Since, 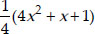and 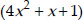have same zeroes, therefore, the required quadratic polynomial is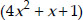
(vi) Since, sum of zeroes, (α + β) = 4 and product of zeroes, αβ = 1
∴ The required quadratic polynomial is
x² - (α + β)x + αβ = x² - 4x + 1

Q 4.

Divide the polynomial p(x ) by the polynomial g(x ) and find the quotient and remainder in each of the following :
(i) p(x ) = x³ - 3 x² + 5 x - 3, g(x ) = x² - 2
(ii) p(x ) = x⁴ - 3 x² + 4 x + 5, g(x ) = x² + 1 - x
(iii) p(x ) = x⁴ - 5 x + 6, g(x ) = 2 - x²

SOLUTION:

Soln. : (i) Here, dividend p(x) = x³ - 3x² + 5x - 3, divisor g(x) = x² - 2
∴ We have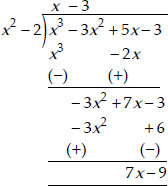

Thus, the quotient = (x - 3)
and remainder = (7x - 9)
(ii) Here, dividend p(x) = x⁴ - 3x² + 4x + 5
and divisor g(x) = x² + 1 - x = x² - x + 1
∴ We have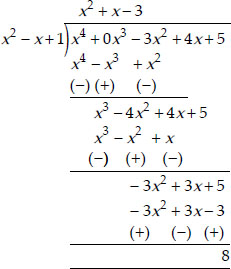

Thus, the quotient is (x² + x - 3) and remainder = 8
(iii) Here, dividend, p(x) = x⁴ - 5x + 6 and divisor, g(x) = 2 - x² = - x² + 2
∴ We have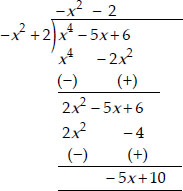

Thus, the quotient = -x² - 2
and remainder = -5x + 10.

Q 5.

Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial :
(i) t² - 3; 2 t⁴ + 3 t³ - 2 t² - 9 t - 12
(ii) x² + 3 x + 1; 3 x⁴ + 5 x³ - 7 x² + 2 x +2
(iii) x³ - 3 x + 1; x⁵ - 4 x³ + x² + 3 x + 1

SOLUTION:

Soln. : (i) Dividing 2t⁴ + 3t³ - 2t² - 9t - 12 by t² - 3, we have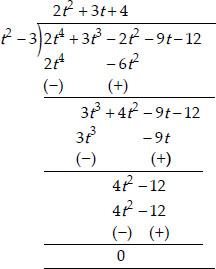

Remainder = 0
∴ (t² - 3) is a factor of 2t⁴ + 3t³ - 2t² - 9t - 12.
(ii) Dividing 3x⁴ + 5x³ - 7x² + 2x + 2 by
x² + 3x + 1, we have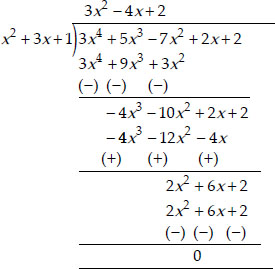

Remainder = 0
∴ x² + 3x + 1 is a factor of 3x⁴ + 5x³ - 7x² + 2x + 2.
(iii) Dividing x⁵ - 4x³ + x² + 3x + 1 by
x³ - 3x + 1, we get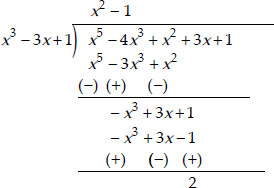

The remainder = 2, i.e., remainder ≠ 0
∴ x³ - 3x + 1 is not a factor of x⁵ - 4x³ + x²
+ 3x + 1.

Q 6.

Obtain all other zeroes of 3 x⁴ + 6 x³ - 2 x² - 10 x - 5, if two of its zeroes are 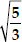and -.

SOLUTION:

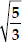Soln. : We have p(x) = 3x⁴ + 6x³ - 2x² - 10x - 5.
Given 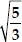and -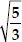 are zeroes of p(x).
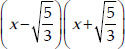∴ is a factor of p(x).
Now, let us divide 3x⁴ + 6x³ - 2x² - 10x - 5 by
.


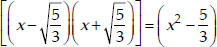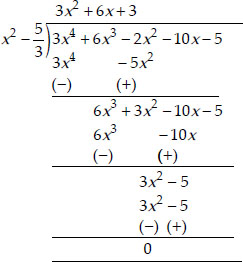
∴ 3x⁴ + 6x³ - 2x² - 10x - 5
= (3x² + 6x +3) (x² - 5/3)
= 3(x² + 2x + 1)
= 3(x + 1)² (x² - 5/3)
Thus, the other zeroes of the given polynomial are -1 and -1.

Q 7.

On dividing x³ - 3 x² + x + 2 by a polynomial g(x ), the quotient and remainder were x - 2 and -2 x + 4 respectively. Find g(x ).

SOLUTION:

Soln. : Here, Dividend, p(x) = x³ - 3x² + x + 2
Divisor = g(x),
Quotient = (x - 2) and Remainder = (-2x + 4)
Since, (Quotient × Divisor) + Remainder
= Dividend
∴ [(x - 2) × g(x)] + [(-2x + 4)] = x³ - 3x² + x + 2
⇒ (x - 2) × g(x) = x³ - 3x² + x + 2 - (-2x + 4)
= x³ - 3x² + x + 2 + 2x - 4
= x³ - 3x² + 3x - 2
∴ g(x) =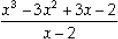
Now, dividing x³ - 3x² + 3x - 2 by x - 2, we have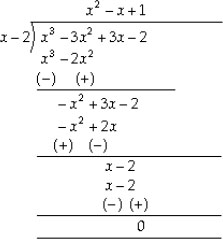

∴ g(x) = 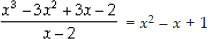= x² - x + 1
Thus, the required divisor g(x) = x² - x + 1.

Q 8.

Give examples of polynomials p(x ), g(x ), q(x ) and r(x ), which satisfy the division algorithm and
(i) deg p(x ) = deg q(x )
(ii) deg q(x ) = deg r(x )
(iii) deg r(x ) = 0

SOLUTION:

Soln. : (i) p(x) = 3x² - 6x + 27,
g(x) = 3 and q(x) = x² - 2x + 9.
Now, deg p(x) = deg q(x)
r(x) = 0
⇒ p(x) = q(x) × g(x) + r(x).
(ii) p(x) = 2x³ - 2x² + 2x + 3,
g(x) = 2x² - 1, q(x) = x - 1 and
r(x) = 3x + 2, deg q(x) = deg r(x)
⇒ p(x) = q(x) × g(x) + r(x)
(iii) p(x) = 2x³ - 4x² + x + 4,
g(x) = 2x² + 1, q(x) = x - 2 and
r(x) = 6, deg r(x) = 0
⇒ p(x) = q(x) × g(x) + r(x)

Q 9.

Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case :
(i) 2 x³ + x² - 5 x + 2; 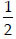, 1, - 2
(ii) x³ - 4 x² + 5 x - 2; 2, 1, 1

SOLUTION:

Soln. : ∴ (i) p(x) = 2x³ + x² - 5x + 2


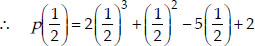
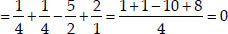
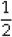⇒ is a zero of p(x).
Again, p(1) = 2(1)³ + (1)² - 5(1) + 2
= 2 + 1 - 5 + 2 = 0
⇒ 1 is a zero of p(x).
Also, p(-2) = 2(-2)³ + (-2)² - 5(-2) + 2
= -16 + 4 + 10 + 2
= -16 + 16 = 0
⇒ - 2 is a zero of p(x).
Now, p(x) = 2x³ + x² - 5x + 2
∴ Comparing it with ax³ + bx² + cx + d, we have a = 2, b = 1, c = - 5 and d = 2
Also 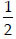, 1 and - 2 are the zeroes of p(x).




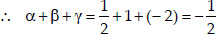
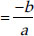
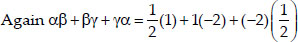
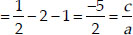
and product of zeroes = αβγ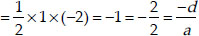

Thus, the relationship between the coefficients and the zeroes of p(x) is verified.
(ii) Here, p(x) = x³ - 4x² + 5x - 2
∴ p(2) = (2)³ - 4(2)² + 5(2) - 2
= 8 - 16 + 10 - 2 = 18 - 18 = 0
⇒ 2 is a zero of p(x)
Again p(1) = (1)³ - 4(1)² + 5(1) - 2
= 1 - 4 + 5 - 2 = 6 - 6 = 0
⇒ 1 is a zero of p(x).
Now, Comparing p(x) = x³ - 4x² + 5x - 2 with ax³ + bx² + cx + d = 0, we have
a = 1, b = - 4, c = 5 and d = - 2
2, 1 and 1 are the zeroes of p(x).
∴ Let α = 2, β = 1, γ = 1
Now, sum of zeroes = α + β + γ
= 2 + 1 + 1 = 4 = -b/a

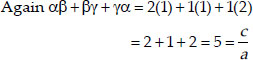
Product of zeroes = αβγ = (2)(1)(1) = 2 = -d/a
Thus, the relationship between the zeroes and the coefficients of p(x) is verifed.

Q 10.

Find a cubic polynomial with the sum, sum of products of its zeroes taken two at a time and the product of its zeroes as 2, -7, -14 respectively.

SOLUTION:

Soln. : Let the required cubic polynomial be ax³ + bx² + cx + d and its zeroes be α, β and γ.



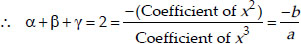
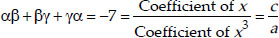
If a = 1, then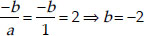

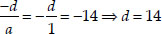
and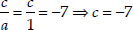
∴ The required cubic polynomial is
1x³ + (-2)x² + (-7)x + 14
= x³ - 2x² - 7x + 14.

Q 11.

If the zeroes of the polynomial x³ - 3 x² + x + 1 are a - b , a , a + b , find a and b .

SOLUTION:

Soln. : We have p(x) = x³ - 3x² + x + 1.
Comparing it with Ax³ + Bx² + Cx + D,
We have A = 1, B = -3, C = 1 and D = 1
It is given that (a - b), a and (a + b) are the zeroes of the polynomial.
∴ Let α = (a - b), β = a and γ = (a + b)

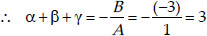
⇒ (a - b) + a + (a + b) = 3
⇒ 3a = 3
⇒ a = 1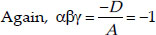

⇒ (a - b) × a × (a + b) = -1
⇒ (1 - b) × 1 × (1 + b) = -1
⇒ 1 - b² = -1
⇒ b² = 1 + 1 = 2
Thus, a = 1 and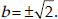

Q 12.

If two zeroes of the polynomial
x⁴ - 6 x³ - 26 x² + 138 x - 35 are 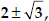find other zeroes.

SOLUTION:

Soln. : Here, p(x) = x⁴ - 6x³ - 26x² + 138x - 35
∵ Two of the zeroes of p(x) are :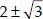



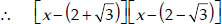
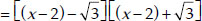
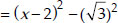
= (x² + 4 - 4x) - 3 = x² - 4x + 1
or x² - 4x + 1 is a factor of p(x).
Now, dividing p(x) by x² - 4x + 1, we have

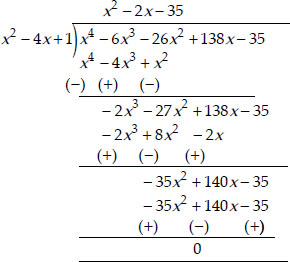
∴ (x² - 4x + 1)(x² - 2x - 35) = p(x)
⇒ (x² - 4x + 1)(x - 7)(x + 5) = p(x)
i.e., (x - 7) and (x + 5) are other factors of p(x).
∴ 7 and - 5 are other zeroes of the given polynomial.

Q 13.

If the polynomial x⁴ - 6 x³ + 16 x² - 25 x + 10 is divided by another polynomial x² - 2 x + k , the remainder comes out to be ( x + a ), find k and a .

SOLUTION:

Soln. : Applying the division algorithm to the polynomials x⁴ - 6x³ + 16x² - 25x + 10 and x² - 2x + k, we have

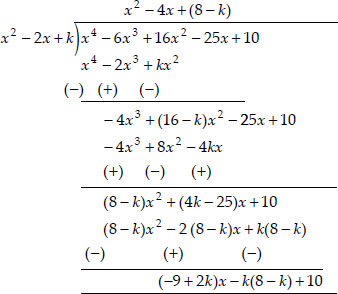
∴ Remainder = (2k - 9)x - k(8 - k) + 10
But the remainder = x + a
Therefore, comparing them, we have
2k - 9 = 1 ⇒ 2k = 1 + 9 = 10
⇒
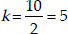
and a = - k(8 - k) + 10
= - 5(3) + 10 = - 15 + 10 = - 5
Thus, k = 5 and a = - 5