Q 1.

In each of the following, give the justification of the construction also.
Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.

SOLUTION:

Soln. : Steps of Construction :
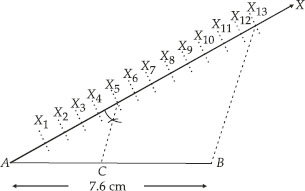
I. Draw a line segment AB = 7.6 cm.
II. Draw a ray AX making an acute angle with AB.
III. Mark 13 (8 + 5) equal points on AX, and mark them as X₁, X₂, X₃, ........, X₁₃.
IV. Join points X₁₃ and B.
V. From point X₅, draw X₅C || X₁₃B, which meets AB at C.
Thus, C divides AB in the ratio 5 : 8
On measuring the two parts, we get
AC = 2.9 cm and CB = 4.7 cm.

Justification:
In ∆ABX₁₃ and ∆ACX₅, we have
CX₅ || BX₁₃
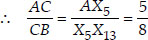[By Thales theorem]
⇒ AC : CB = 5 : 8.

Q 2.

In each of the following, give the justification of the construction also.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are of the corresponding sides of the first triangle.

SOLUTION:

Soln. : Steps of Construction :
I. Draw a ∆ABC such that BC = 6cm, AC = 5 cm and AB = 4 cm.
II. Draw a ray BX making an acute angle ∠CBX.
III. Mark three points X₁, X₂, X₃ on
BX such that BX₁ = X₁X₂ = X₂X₃.

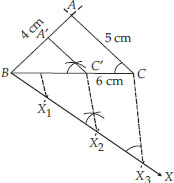
IV. Join X₃C.
V. Draw a line through X₂ such that it is parallel to X₃C and meets BC at C'.
VI. Draw a line through C' parallel to CA to intersect BA at A'.
Thus, A'BC' is the required similar triangle.
Justification:
By construction, we have X₃C || X₂C'
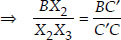[Using Thales theorem]


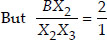
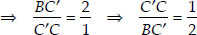
Adding 1 to both sides, we get



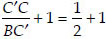
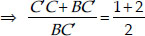
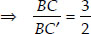
Now, in ∆BC′A′ and ∆BCA, we have CA ||C′A′
∴ Using AA similarity, we have
∆BC′A′ ~ ∆BCA

Q 3.

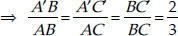
In each of the following, give the justification of the construction also.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are of the corresponding sides of the first triangle.

SOLUTION:

Soln. : Steps of Construction :
I. Construct a ∆ABC such that AB = 5 cm,
BC = 7 cm and AC = 6 cm.

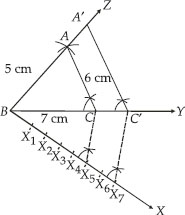
II. Draw a ray BX such that ∠CBX is an acute angle.
III. Mark 7 points of X₁, X₂, X₃, X₄, X₅, X₆ and X₇ on BX such that BX₁ = X₁X₂ =X₂X₃ = X₃X₄ = X₄X₅ = X₅X₆ = X₆X₇
IV. Join X₅ to C.
V. Draw a line through X₇ intersecting BC (produced) at C′ such that X₅C || X₇C′
VI. Draw a line through C′ parallel to CA to intersect BA (produced) at A′.
Thus, ∆A'BC' is the required triangle.
Justification:
By construction, we have C′A′ || CA
∴ Using AA similarity, ∆ABC ~ ∆A'BC'

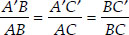
Also X₇C′ || X₅C      [By construction]
∴ ∆BX₇C' ~ ∆BX₅C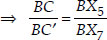

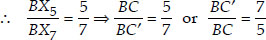
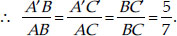
Q 4.

In each of the following, give the justification of the construction also.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 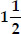times the corresponding sides of the isosceles triangle.

SOLUTION:

Soln. : Steps of Construction :
I. Draw BC = 8 cm
II. Draw the perpendicular bisector of BC which intersects BC at D.

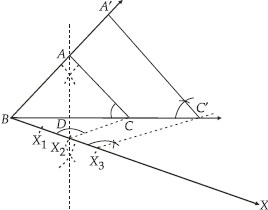
III. Mark a point A on the above perpendicular such that DA = 4 cm.
IV. Join AB and AC.
Thus, ∆ABC is the required isosceles triangle.
V. Now, draw a ray BX such that ∠CBX is an acute angle.
VI. On BX, mark three points X₁, X₂ and X₃ such that:
BX₁ = X₁X₂ = X₂X₃
VII. Join X₂C.
VIII. Draw a line through X₃ parallel to X₂C and intersecting BC (extended) to C′.
IX. Draw a line through C′ parallel to CA intersecting BA (extended) to A′, thus,
∆A'BC' is the required triangle.
Justification:
We have C′A′ || CA      [By construction]
∴ Using AA similarity, ∆A′BC′ ~ ∆ABC
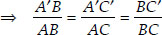...(i)
Since, In ∆BX₃C′, X₃C′ || X₂C       [By construction]
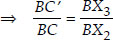      [By BPT]


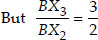
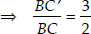
Thus, By (i)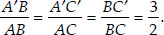

Q 5.

In each of the following, give the justification of the construction also.
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then costruct a triangle whose sides are of the corresponding sides of the triangle ABC.

SOLUTION:

Soln. : Steps of construction:
I. Construct a ∆ABC such that BC = 6 cm, AB = 5 cm and ∠ABC = 60°.
II. Draw a ray BX such that ∠CBX is an acute angle.

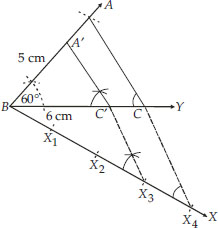
III. Mark four points in a line through X₃, parallel to X₄C to intersect BC at C′
BX₁ = X₁X₂ = X₂X₃ = X₃X₄
IV. Join X₄C and draw a line through X₃ parallel to X₄C to intersect BC at C'.
V. Also draw another line through C' and parallel to CA to intersect BA at A'.
Thus, ∆A'BC' is the required triangle.
Justification:
In ∆BX₄C we have
X₄C || X₃C'      [By construction]
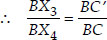      [By BPT]
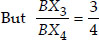      [By construction]
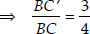      ...(i)
Now, we also have
CA || C'A'      [By construction]
∴ ∆BC'A' ~ ∆BCA      [using AA similarity]
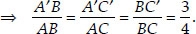[From (i)]

Q 6.

In each of the following, give the justification of the construction also.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are times the corresponding sides of ∆ABC.

SOLUTION:

Soln. : Steps of Construction:
I. Construct a ∆ABC such that BC = 7 cm, ∠B = 45°, ∠A = 105° and ∠C = 30°
II. Draw a ray BX making an acute angle ∠CBX with BC.

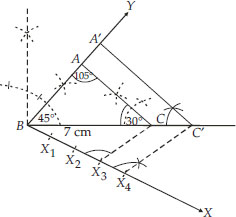
III. On BX, mark four points X₁, X₂, X₃ and X₄ such that
BX₁ = X₁X₂ = X₂X₃ = X₃X₄.
IV. Join X₃C.
V. Draw a line through X₄ parallel to X₃C intersecting BC(extended) at C′
VI. Draw a line through C′ parallel to CA intersecting the extended line segment BA at A′.
Thus, ∆A′BC′ is the required triangle.
Justification:
By construction, we have
C′A′ || CA
∴ ∆ABC ~ ∆A′BC′      [AA similarity]
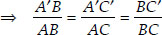      ...(i)
Also, In ∆BX₄C′,
X₄C′ || X₃C       [By construction]
∴ ∆BX₄C′ ~ ∆BX₃C      [AA similarity]


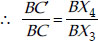
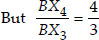
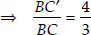      ...(ii)
From (i) and (ii), we have

Q 7.

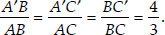
In each of the following, give the justification of the construction also.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are times the corresponding sides of the given triangle.

SOLUTION:

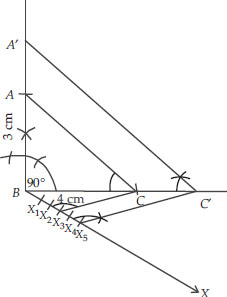
Soln. : Steps of Construction:
I. Construct the right triangle ABC such that ∠B = 90°, BC = 4 cm and BA = 3 cm.
II. Draw a ray BX such that an acute angle ∠CBX is formed.
III. Mark 5 points X₁, X₂, X₃, X₄ and X₅ on BX such that BX₁ = X₁X₂ = X₂X₃ = X₄X₅.
IV. Join X₃C.
V. Draw a line through X₅ parallel to X₃C, intersecting the extended line segment BC at C'.
VI. Draw another line through C′ parallel to CA intersecting the extended line segment BA at A'.
Thus, ∆A′BC′ is the required triangle.
Justification:
By construction, we have:
C′A′ || CA
∴ ∆ABC ~ ∆A′BC′      [AA similarity]
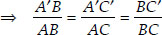      ...(i)

Also, in ∆BX₅C′, X₅C′ || X₃C   [By construction]
∴ ∆BX₅C′ ~ ∆BX₃C      [AA similarity]

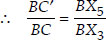
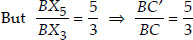      ...(ii)
From (i) and (ii), we get

Q 8.

In each of the following, give also the justification of the construction:
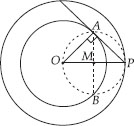
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.

SOLUTION:

Soln. : Steps of Construction:
I. Draw a circle of radius 6 cm. Let its centre be O.
II. Take a point P such that OP = 10 cm. Join OP.

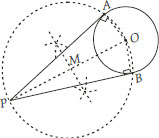
III. Bisect OP and let M be its midpoint.
IV. Taking M as centre and MP or MO as radius draw a circle.
Let the new circle intersects the given circle at A and B. Join PA and PB.
Thus, PA and PB are the required tangents.
By measurement, we have : PA = PB = 8 cm.
Justification:
Join OA and OB
Since PO is a diameter.
∴ ∠OAP = 90° = ∠OBP
[Angles in a semicircle]
Also, OA and OB are radii of the same circle.
⇒ PA and PB are tangents to the circle.

Q 9.

In each of the following, give also the justification of the construction:
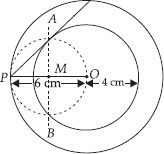
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.

SOLUTION:

Soln. : Steps of Construction :
I. Draw two concentric circles with centre O and radii 4 cm and 6 cm.
II. Take any point P on outer circle.
III. Join PO and bisect it and let the midpoint of PO is represented by M.
IV. Taking M as centre and OM or MP as radius, draw a circle such that this circle intersects the circle (of radius 4 cm) at A and B.
V. Join AP. Thus, PA is the required tangent.
By measurement, we have PA = 4.5 cm

Justification:
Join OA. As PO is diameter
∴ ∠PAO = 90° [Angle in a semi-circle]
⇒ PA ┴ OA
∵ OA is a radius of the inner circle.
∴ PA has to be a tangent to the inner circle. Verification of length of PA. In right ∆PAO, PO = 6 cm, OA = 4 cm.


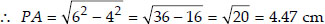
Hence both lengths are approximately equal.

Q 10.

In each of the following, give also the justification of the construction:
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameters each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.

SOLUTION:

Soln. : Steps of Construction :
I. Draw a circle of radius 3 cm with centre O and draw a diameter.
II. Extend its diameter on both sides and cut OP = OQ = 7 cm
III. Bisect PO such that M be its mid-point.
IV. Taking M as centre and MO as radius, draw a circle. Let it intersect the given circle at A and B.
V. Join PA and PB.
Thus, PA and PB are the two required tangents from P.
VI. Now bisect OQ such that N is its mid point.
VII. Taking N as centre and NO as radius, draw a circle. Let it intersect the given circle at C and D.
VIII.Join QC and QD.
Thus, QC and QD are the required tangents from Q.

Justification :
Join OA to get ∠OAP = 90°
            [Angle in a semi-circle]
⇒ PA ┴ OA ⇒ PA is a tangent.
Similarly, PB ┴ OA ⇒ PB is a tangent.
Now, join OC to get ∠QCO = 90° [Angle in a semi-circle]
⇒ QC ┴ OC ⇒ QC is a tangent.
Similarly, QD ┴ OC ⇒ QD is a tangent.

Q 11.

In each of the following, give also the justification of the construction:
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.

SOLUTION:

Soln. : Steps of Construction :
I. With centre O and radius = 5 cm, draw a circle.
II. Taking a point A on the circle draw ∠AOB = 120°.

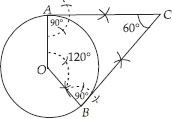
III. Draw a perpendicular on OA at A.
IV. Draw another perpendicular on OB at B.
V. Let the two perpendiculars meet at C.
Thus CA and CB are the two required tangents to the given circle which are inclined to each other at 60°.
Justification:
In a quadrilateral OACB, using angle sum property, we have
120° + 90° + 90° + ∠ACB = 360°
⇒ 300° + ∠ACB = 360°
⇒ ∠ACB = 360° - 300° = 60°.

Q 12.

In each of the following, give also the justification of the construction:
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.

SOLUTION:

Soln. : Steps of Construction:
I. Draw a line segment AB = 8 cm
II. Draw a circle with centre A and radius 4 cm, draw another circle with centre B and radius 3 cm.
III. Bisect the line segment AB. Let its mid point be M.
IV. With centre as M and MA (or MB) as radius, draw a circle such that it intersects the two circles at points P, Q, R and S.
V. Join BP and BQ.
Thus, BP and BQ are the required two tangents from B to the circle with centre A.
VI. Join RA and SA.
Thus, RA and SA are the required two tangents from A to the circle with centre B.

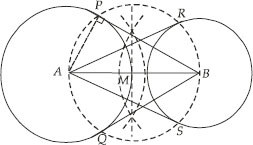
Justification:
Let us join A and P.
∵ ∠APB = 90° [Angle in a semi-circle]
∴ BP ┴ AP
But AP is radius of the circle with centre A.
⇒ BP has to be a tangent to the circle with centre A.
Similarly,
BQ has to be tangent to the circle with centre A.
Also AR and AS are tangents to the circle with centre B.

Q 13.

In each of the following, give also the justification of the construction:
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. B∆ is the perpendicular from B on AC. The circle through B, C, ∆ is drawn. Construct the tangents from A to this circle.

SOLUTION:

Soln. : Steps of construction:
I. Draw ∆ABC such that AB = 6 cm, BC = 8 cm and ∠B = 90°.
II. Draw BD ┴ AC. Now bisect BC and let its midpoint be O.
So O is centre of the circle passing through B, C and D.

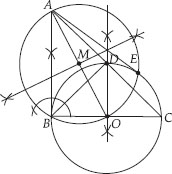
III. Join AO
IV. Bisect AO. Let M be the mid-point of AO.
V. Taking M as centre and MA as radius, draw a circle intersecting the given circle at B and E.
VI. Join AB and AE. Thus, AB and AE are the required two tangents to the given circle from A.
Justification:
Join OE, then ∠AEO = 90°
[Angle in a semi circle]
∴ AE ┴ OE.
But OE is a radius of the given circle.
⇒ AE has to be a tangent to the circle.
Similarly, AB is also a tangent to the given circle.

Q 14.

In each of the following, give also the justification of the construction:
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.

SOLUTION:

Soln. : Steps of Construction:
I. Draw the given circle using a bangle.
II. Take two non parallel chords PQ and RS of this circle.

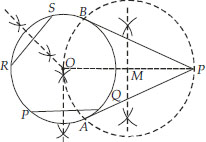
III. Draw the perpendicular bisectors of PQ and RS such that they intersect at O. Therefore, O is the centre of the given circle.
IV. Take a point P outside this circle.
V. Join OP and bisect it. Let M be the mid-point of OP.
VI. Taking M as centre and OM as radius, draw a circle. Let it intersect the given circle at A and B.
VII. Join PA and PB. Thus, PA and PB are the required two tangents.
Justification :
Join OA and OB.
Since ∠OAP = 90° [Angle in a semi circle]
∴ PA ┴ OA.
Also OA is a radius.
∴ PA has to be a tangent to the given circle.
Similarly, PB is also a tangent to the given circle.