Q 1.

Construct an angle of 90° at the initial point of a given ray and justify the construction.

SOLUTION:

Steps of Construction :
Step I : Draw a ray .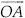
Step II : Taking O as centre and suitable radius, draw a semicircle, which cuts OA at B.
Step III : Keeping the radius same, divide the semicircle into three equal parts such that
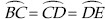
Step IV : Draw .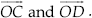
Step V : Draw 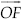, the bisector of ∠COD.
Thus, ∠AOF = 90°

Justification :
O is the centre of the semicircle and it is divided into 3 equal parts.
Therefore,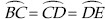
⇒ ∠BOC = ∠COD = ∠DOE [Equal chords subtend equal angles at the centre]
∠BOC + ∠COD + ∠DOE = 180°
⇒ ∠BOC + ∠BOC + ∠BOC = 180°
⇒ 3∠BOC = 180° ⇒ ∠BOC = 60°
Similarly, ∠COD = 60° and ∠DOE = 60°
OF is the bisector of ∠COD

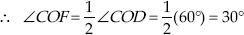
Now, ∠BOC + ∠COF = 60° + 30°
⇒ ∠BOF = 90° or ∠AOF = 90°

Q 2.

Construct an angle of 45° at the initial point of a given ray and justify the construction.

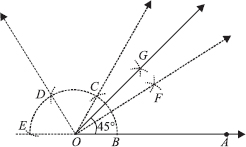
SOLUTION:

Steps of Construction :
Step I : Draw a ray .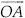
Step II : Taking O as centre and with a suitable radius, draw a semi
circle such that it intersects 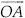at B.
Step III : Taking B as centre and keeping the same radius, cut the semicircle at C. Now, taking C as centre and keeping the same radius, cut the semicircle at D and similarly, cut at E, such that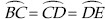

Join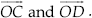
Step IV : Draw 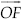, the angle bisector of ∠BOC.
Step V : Draw 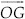, the angle bisector of ∠FOC.
Thus, ∠BOG = 45° or ∠AOG = 45°

Justification :

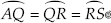
⇒ ∠BOF + ∠FOG = 45° [∵ ∠COF = ∠BOF]
⇒ ∠BOG = 45°

Q 3.

Construct the angles of the following measurements.
(i) 30°
(ii) 22½°
(iii) 15°

SOLUTION:

(i) Angle of 30°
Steps of Construction :
Step I : Draw a ray .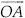
Step II : With O as centre and having a suitable radius, draw an arc cutting 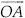at B.
Step III : With centre at B and the same radius as above, draw an arc to cut the previous arc at C.
Step IV : Join 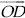which gives ∠BOC = 60°.
Step V : Draw 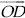, bisector of ∠BOC, such

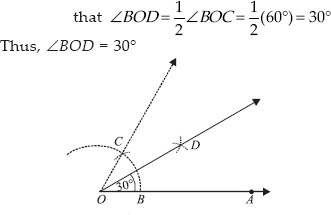
(ii) 22½°
Steps of Construction :
Step I : Draw a ray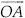
Step II : Construct ∠AOB = 90°
Step III : Draw 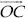, the bisector of ∠AOB, such that

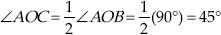
Step IV : Now, draw 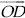, the bisector of ∠AOC, such that


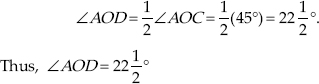
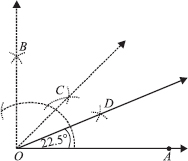
(iii) Angle of 15°
Steps of Construction :
Step I : Draw a ray .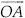
Step II : Construct ∠AOB = 60°
Step III : Draw 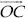, the bisector
of ∠AOB, such that

Q 4.

Construct the following angles and verify by measuring them by a protractor.
(i) 75°
(ii) 105°
(iii) 135°

SOLUTION:

(i) Steps of Construction :
Step I : Draw a ray .
Step II : With O as centre and having a suitable radius, draw an arc which cuts at B.
Step III : With centre B and keeping the radius same, mark a point C on the previous arc.
Step IV : With centre C and having the same radius, mark another point D on the arc of step II.

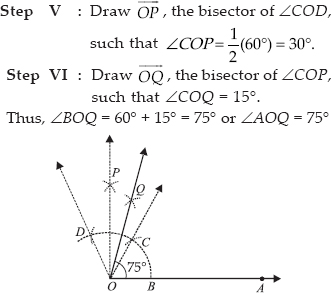
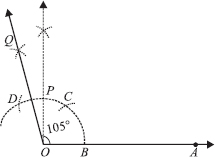
(ii) Steps of Construction :
Step I : Draw a ray .
Step II : With centre O and having a suitable radius, draw an arc which cuts at B.
Step III : With centre B and keeping the same radius, mark a point C on the arc of step II.
Step IV : With centre C and having the same radius, mark another point
D on the arc drawn in step II.
Step V : Draw , the bisector of
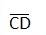
Step VI : Draw 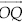, the bisector of
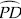
Thus, ∠AOQ = 90° + 15° = 105°

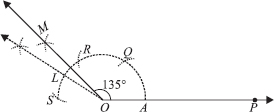
(iii) Steps of Construction :
Step I : Draw a ray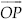
Step II : With centre O and having a suitable radius, draw an arc which cuts OP at A.
Step III : Keeping the same radius and starting from A, mark points Q, R and S on the arc of step II such that
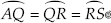
Step IV : Draw 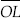, the bisector of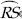
Step V : Draw 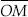, the bisector of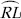
Thus, ∠POM = 135°

Q 5.

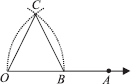
Construct an equilateral triangle, given its side and justify the construction.

SOLUTION:

Let us construct an equilateral triangle, each of whose side = 3 cm(say).
Steps of Construction :
Step I :Draw a ray .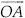
Step II :Taking O as centre and radius equal to 3 cm, draw an arc to cut 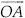at B such that OB = 3 cm
Step III : Taking B as centre and radius equal to OB, draw an arc, to intersect the previous arc at C.
Step IV : Join OC and OB.
Thus, ∆OBC is the required equilateral triangle.

Justification :
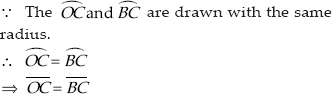[Chords corresponding to equal arcs are equal]
OC = OB = BC
∴ ∆OBC is an equilateral triangle.

Q 6.

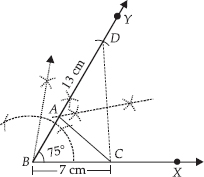
Construct a triangle ABC in which BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.

SOLUTION:

Step I Draw a ray .
Step II : Along , cut off a line segment
BC = 7 cm.
Step III : At B, construct ∠CBY = 75°
Step IV : From 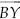, cut off BD = 13 cm
(= AB + AC)
Step V : Join DC.
Step VI : Draw perpendicular bisector of CD which meets BD at A.
Step VII :Join AC.
Thus, ∆ABC is the required triangle.

Q 7.

Construct a triangle ABC in which BC = 8 cm, ∠B = 45° and AB – AC = 3.5 cm.

SOLUTION:

Steps of Construction:
Step I : Draw a ray .
Step II : Along , cut off a line segment BC = 8 cm.
Step III : Construct ∠CBY = 45°
Step IV : From BY, cut off BD = 3.5 cm.
Step V : Join DC.
Step VI : Draw PQ, perpendicular bisector of DC, which intersects 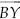at A.
Step VII : Join AC.
Thus, ABC is the required triangle.

Q 8.

Construct a triangle PQR in which QR = 6 cm, ∠Q = 60° and PR – PQ = 2 cm.

SOLUTION:

Steps of Construction:
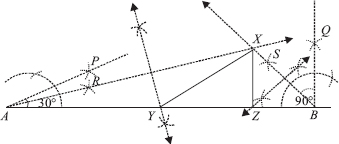
Step I : Draw a ray .
Step II : Along 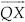, cut a line segment QR = 6 cm.
Step III : Construct a line YQY ′ such that ∠RQY = 60°.
Step IV : Cut off QS = 2 cm on QY ′.
Step V : Join SR.
Step VI : Draw MN, perpendicular bisector of SR, which intersects QY at P.
Step VII : Join PR.
Thus, ∆PQR is the required triangle.

Q 9.

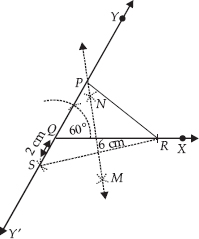
Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.

SOLUTION:

Steps of Construction:
Step I : Draw a line segment AB = 11 cm = (XY + YZ + ZX)
Step II : Construct ∠BAP = 30°
Step III : Construct ∠ABQ = 90°
Step IV : Draw AR, the bisector of ∠BAP.
Step V : Draw BS, the bisector of ∠ABQ. Let AR and BS intersect at X.
Step VI : Draw perpendicular bisector of AX, which intersects AB at Y.
Step VII : Draw perpendicular bisector of XB, which intersects AB at Z.
Step VIII : Join XY and XZ.
Thus, ∆XYZ is the required triangle.

Q 10.

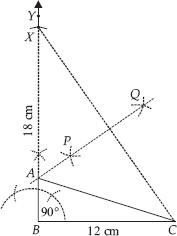
Construct a right triangle whose base is
12 cm and sum of its hypotenuse and other side is 18 cm.

SOLUTION:

Steps of Construction:
Step I : Draw BC = 12 cm.
Step II : Construct ∠CBY = 90°
. Step III : Along 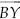, cut a line segment
BX = 18 cm.
Step IV : Join CX.
Step V : Draw PQ, perpendicular bisector of CX, which meets BX at A.
Step VI : Join AC.
Thus, ∆ABC is the required triangle.