Squares and Square Roots (Mathematics) Class 8 - NCERT Questions
What will be the unit digit of the squares of the following numbers?
(i) 81
(ii) 272
(iii) 799
(iv) 3853
(v) 1234
(vi)
26387
(vii) 52698
(viii) 99880
(ix) 12796
(x) 55555.
(i) The unit digit of (81)2 is 1.
Because when we multiply the unit digit 1 by itself, we get 1.
(ii) The unit digit of (272)2 is 4.
Because when we multiply the unit digit 2 by itself, we get 4.
(iii) The unit digit of (799)2 is 1.
Because when we multiply the unit digit 9 by itself, we get 81.
(iv) The unit digit of (3853)2 is 9.
Because when we multiply the unit digit 3 by itself, we get 9.
(v) The unit digit of (1234)2 is 6.
Because when we multiply the unit digit 4 by itself, we get 16.
(vi) The unit digit of (26387)2 is 9.
Because when we multiply the unit digit 7 by itself, we get 49.
(vii) The unit digit of (52698)2 is 4.
Because when we multiply the unit digit 8 by itself, we get 64.
(viii) The unit digit of (99880)2 is 0.
Because when we multiply the unit digit 0 by itself, we get 0.
(ix) The unit digit of (12796)2 is 6.
Because when we multiply the unit digit 6 by itself, we get 36.
(x) The unit digit of (55555)2 is 5.
Because when we multiply the unit digit 5 by itself, we get 25.
The following numbers are obviously not perfect squares. Give reason.
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 64000
(vi) 89722
(vii) 222000
(viii) 505050.
We know that number ending in 2, 3, 7 or 8 are not perfect squares.
(i) 1057 (ii) 23453 (iii) 7928
(iv) 222222 (vi) 89722
Clearly, all ends with the digits 7, 3, 8, 2.
∴ These are not perfect squares.
Since, for perfect squares, there should be even number of zeroes at the end.
(v) 64000 (vii) 222000 (viii) 505050
Clearly, all ends with the odd number of zeroes.
So, they are not perfect squares.
The square of which of the following would be odd numbers ?
(i) 431
(ii) 2826
(iii) 7779
(iv) 82004.
(i) When we multiply the unit digit 1 by itself, we get 1 at the end, which shows that the square of 431 is an odd number.
(ii) When we multiply the unit digit 6 by itself we get 36, i.e., we get 6 at the end, which is an even number.
(iii) When we multiply the unit digit 9 by itself we get 81, i.e. the square of 7779 gives us 1 at the end. So, the square of 7779 is an odd number.
(iv) When we multiply the unit digit 4 by itself we get 16, i.e., we get 6 at the end, which is an even number.
Observe the following pattern and find the missing digits.
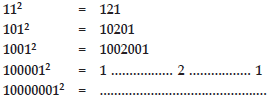
1000012 = 10000200001 100000012 = 100000020000001.
Q 5.Observe the following pattern and supply the missing numbers.
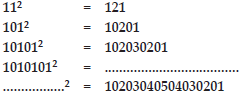
10101012 = 1020304030201
1010101012 = 10203040504030201.
Using the given pattern, find the missing numbers.
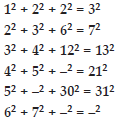
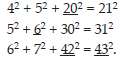
Without adding, find the sum.
(i) 1 + 3 + 5 + 7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23.
(i) We have to find the sum of first 5 odd numbers,
1 + 3 + 5 + 7 + 9 = 52 = 25.
(ii) We have to find the sum of the first 10 odd numbers,
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 102 = 100.
(iii) We have to find the sum of first 12 odd numbers,
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 = 122 = 144.
(i) Express 49 as the sum of 7 odd numbers.
(ii) Express 121 as the sum of 11 odd numbers.
(i) 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13.
(ii) 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21.
How many numbers lie between squares of the following numbers?
(i) 12 and 13
(ii) 25 and 26
(iii) 99 and 100.
(i) We have to find the number of terms between the squares of 12 and 13, by doubling the first term from 12 and 13. i.e., 2 × 12 = 24.
∴ Total number of terms = 24.
(ii) We can find the number of terms between the squares of 25 and 26, by doubling the first term from 25 and 26. i.e., 2 × 25 = 50.
∴ Total number of terms = 50.
(iii) We can find the number of terms between the squares of 99 and 100, by doubling the first term from 99 and 100. i.e., 2 × 99 = 198.
∴ Total number of terms = 198.
Find the square of the following numbers.
(i) 32
(ii) 35
(iii) 86
(iv) 93
(v) 71
(vi) 46.
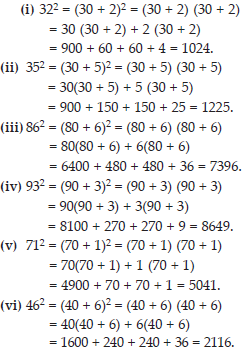
Write a Pythagorean triplet whose one member is
(i) 6 (ii) 14 (iii) 16 (iv) 18.

What could be the possible ‘ones’ digits of the square root of each of the following numbers?
(i) 9801 (ii) 99856
(iii) 998001 (iv) 657666025.
(i) We know that the 'ones' place of the square of 1 and 9 is 1.
∴ The possible ‘ones’ digit of the square root are 1 and 9.
(ii) We know that the ‘ones’ place of the square of 4 and 6 is 6.
∴ The possible ‘ones’ digits of the square root of 99856 are 4 and 6.
(iii) We know that the ‘ones’ place of the square of 1 and 9 is 1.
∴ The possible ‘ones’ digit of the square root of 998001 are 1 and 9.
(iv) We know that ‘ones’ place of the square of 5 is 5.
∴ The possible ‘ones’ digit of the square root of 657666025 is 5.
Without doing any calculation, find the numbers which are surely not perfect squares.
(i) 153 (ii) 257
(iii) 408 (iv) 441.
We know that the numbers ending with 2, 3, 7 or 8 are not perfect squares. So, (i), (ii) and (iii) are surly not perfect squares. (iv) Since, the number 441 ends with 1. Thus, 441 may or may not be a perfect square.
Q 14.Find the square root of 100 and 169 by the method of repeated subtraction.
SOLUTION: 
Find the square roots of the following numbers by the Prime Factorisation Method.
(i) 729 (ii) 400 (iii) 1764
(iv) 4096 (v) 7744 (vi) 9604
(vii) 5929 (viii) 9216 (ix) 529
(x) 8100.

For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained. (i) 252 (ii) 180 (iii) 1008 (iv) 2028 (v) 1458 (vi) 768.
SOLUTION: 
For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also find the square root of the square number so obtained.
(i) 252 (ii) 2925 (iii) 396
(iv) 2645 (v) 2800 (vi) 1620.
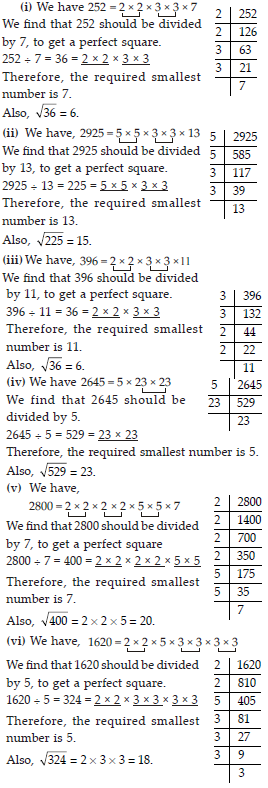
The students of Class VIII of a school donated ` 2401 in all, for the Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
SOLUTION: 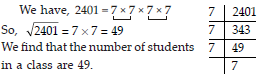
2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
SOLUTION: 
Find the smallest square number that is divisible by each of the numbers 4, 9 and 10.
SOLUTION: 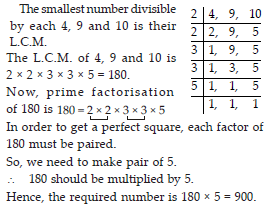
Find the smallest square number that is divisible by each of the numbers 8, 15 and 20.
SOLUTION: 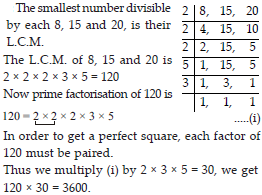
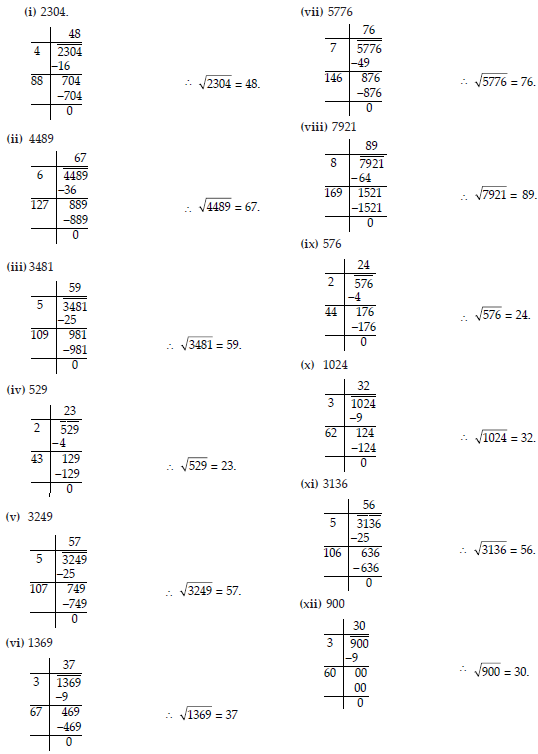
Find the square root of each of the following numbers by Division method.
(i) 2304 (ii) 4489 (iii) 3481
(iv) 529 (v) 3249 (vi) 1369
(vii) 5776 (viii) 7921 (ix) 576
(x) 1024 (xi) 3136 (xii) 900.
Find the number of digits in the square root of each of the following numbers (without any calculation).
(i) 64 (ii) 144 (iii) 4489
(iv) 27225 (v) 390625.

Find the square root of the following decimal numbers.
(i) 2.56 (ii) 7.29 (iii) 51.84
(iv) 42.25 (v) 31.36.

Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 402 (ii) 1989 (iii) 3250
(iv) 825 (v) 4000.
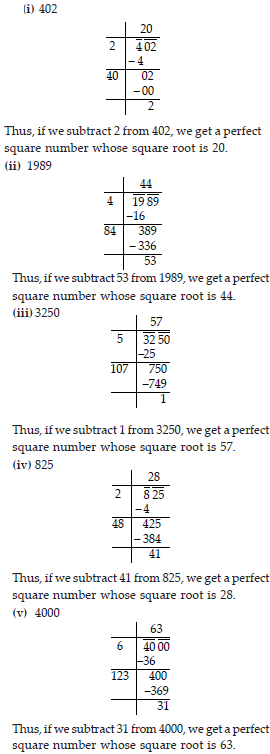
Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 525 (ii) 1750 (iii) 252
(iv) 1825 (v) 6412.

Find the length of the side of a square whose area is 441 m2.
SOLUTION: 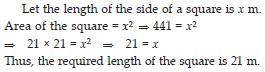
In a triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC.
(b) If AC = 13 cm, BC = 5 cm, find AB.

A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remains same. Find the minimum number of plants he needs more for this.
SOLUTION: 
There are 500 children in a school. For a P.T. drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children would be left out in this arrangement.
SOLUTION: 