Practical Geometry (Mathematics) Class 8 - NCERT Questions
Construct the following quadrilaterals.

(i) Steps of Construction :
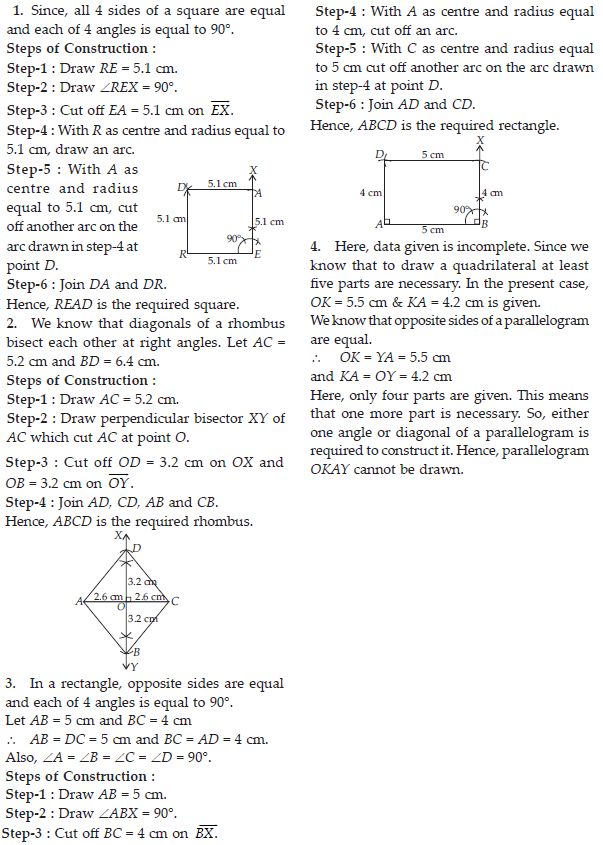
Step-1 : Draw AB = 4.5 cm.
Step-2 : With B as centre and radius equal to 5.5 cm, cut an arc.
Step-3 : With A as centre and radius equal to 7 cm, cut another arc on the arc drawn in step-2 at point C.
Step-4 : With C as centre and radius equal to 4 cm, cut off an arc. Also, with A as centre and radius equal to 6 cm cut off another arc on the arc just drawn at point D.
Step-5 : Join BC, AC, CD and AD.
Hence, ABCD is the required quadrilateral. 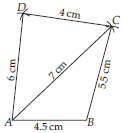
(ii) Steps of Construction :
Step-1 : Draw JU = 3.5 cm.
Step-2 : With J as centre and radius equal to 4.5 cm, cut an arc.
Step-3 : With U as centre and radius equal to 6.5 cm, cut another arc on the arc drawn in step-2 at point P.
Step-4 : With P as centre and radius equal to 5 cm, cut off an arc.
Step-5 : With U as centre and radius equal to 4 cm, cut another arc on the arc drawn in step-4 at point M.
Step-6 : Join JP, UP, UM and PM.
Thus, JUMP is the required quadrilateral.
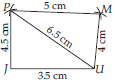
(iii) We know that opposite sides of a parallelogram are equal and parallel to each other.
OR = ME and MO = ER.
Steps of Construction :
Step-1 : Draw OR = 6 cm.
Step-2 : With R as centre and radius equal to 4.5 cm, cut an arc.
Step-3 : With O as centre and radius equal to 7.5 cm, cut another arc on the arc drawn in step-2 at point E.
Step-4 : With E as centre and radius equal to 6 cm, cut an arc.
Step-5 : With O as centre and radius equal to 4.5 cm, cut an arc on the arc drawn in step-4 at point M.
Step-6 : Join RE, OE, OM and ME.
Hence, MORE is the required parallelogram.
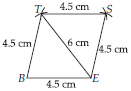
(iv) We know that all four sides of a rhombus are equal.
BE = ES = ST = BT = 4.5 cm.
Steps of Construction :
Step-1 : Draw BE = 4.5 cm.
Step-2 : With B as centre and radius equal to 4.5 cm, draw an arc.
Step-3 : With E as centre and radius equal to 6 cm, draw another arc, cutting the previous arc at point T.
Step-4 : With E as centre and radius equal to 4.5 cm, cut an arc.
Step-5 : With T as centre and radius equal to
4.5 cm, cut another arc on the previous arc at point S.
Step-6 : Join BT, ES, ET and ST.
Hence, BEST is the required rhombus.
Construct the following quadrilaterals.
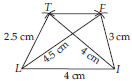
(i) Steps of Construction :
Step-1 : Draw LI = 4 cm.
Step-2 : With L as centre and radius equal to 2.5 cm, cut an arc.
Step-3 : With I as centre and radius equal to
4 cm, cut another arc on the arc drawn in step-2 at point T.
Step-4 : With I as centre and radius equal to 3 cm, cut an arc.
Step-5 : With L as centre and radius equal to
4.5 cm, cut another arc on the arc drawn in step-4 at point F.
Step-6 : Join LT, IT, LF, IF and TF.
Hence, LIFT is the required quadrilateral.
(ii) Steps of Construction :
Step-1 : Draw OL = 7.5 cm.
Step-2 : With L as centre and radius equal to 5 cm cut an arc.
Step-3 : With O as centre and radius equal to 10 cm, cut another arc on the arc drawn in step-2 at point D.
Step-4 : With L as centre and radius equal to 6 cm, cut another arc.
Step-5 : With D as centre and radius equal to 6 cm cut an arc on arc drawn in step-4 at point G.
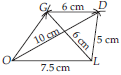
Step-6 : Join LD, LG, OG, OD and DG.
Hence, GOLD is the required quadrilateral.
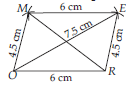
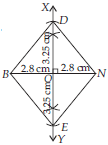
(iii) Here, BN = 5.6 cm and DE = 6.5 cm are given. These two sides are diagonals of a rhombus BEND. We know that diagonals of a rhombus bisect each other at right angles.
Steps of Construction :
Step-1 : Draw BN = 5.6 cm.
Step-2 : Draw perpendicular bisector XY of BN which intersect BN at O.
Step-3 : Cut off OD = OE = 3.25 cm on
Step-4 : Join BD, ND, BE and NE.
Hence, BEND is the required rhombus.
Construct the following quadrilaterals.

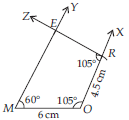
(i) Steps of Construction :
Step-1 : Draw MO = 6 cm.
Step-2 : Make ∠MOX = 105° and ∠OMY = 60°.
Step-3 : Cut off OR = 4.5 cm on OX.
Step-4 : At point R, draw ∠ORZ = 105° which cuts MY at E.
Hence, MORE is the required quadrilateral.
(ii) Here, ∠P = 90°, ∠A = 110°, ∠N = 85°
∠L = 360° – (∠P + ∠A + ∠N)
= 360° – (90° + 110° + 85°)
= 360° – 285° = 75° ...(A)
Steps of Construction :
Step-1 : Draw PL = 4 cm.
Step-2 : Make ∠LPX = 90° and ∠PLY = 75°.
[From (A)]

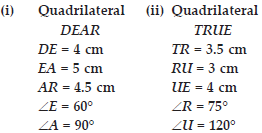
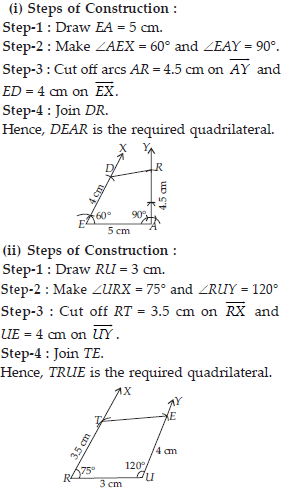
Construct the following quadrilaterals.
Draw the following.
1. The square READ with RE = 5.1 cm.
2. A rhombus whose diagonals are 5.2 cm and 6.4 cm long.
3. A rectangle with adjacent sides of lengths
5 cm and 4 cm.
4. A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm.