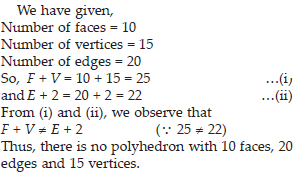Visualising Solid (Mathematics) Class 8 - NCERT Questions
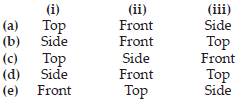
For each of the given solid, the two views are given. Match for each solid the corresponding top and front views. The first one is done for you.
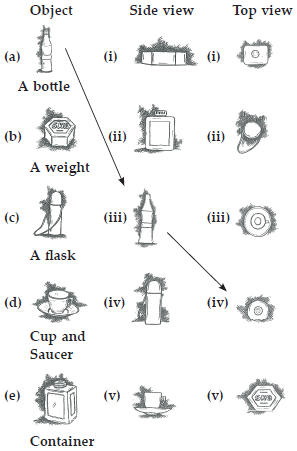

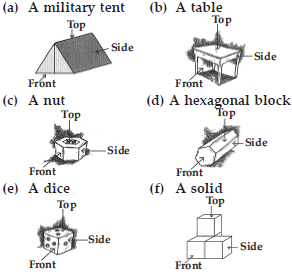
For each of the given solid, the three views are given. Identify for each solid the corresponding top, front and side views.
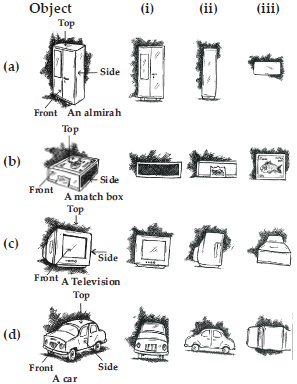

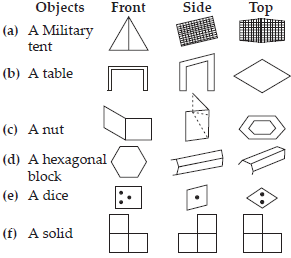
For each given solid, identify the top view, front view and side view
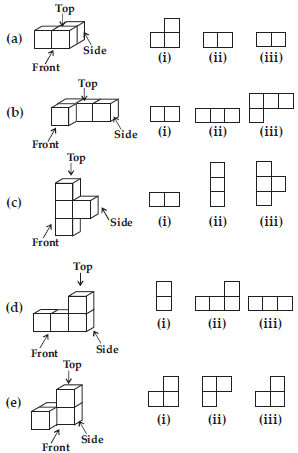
Draw the front view, side view and top view of the given objects.
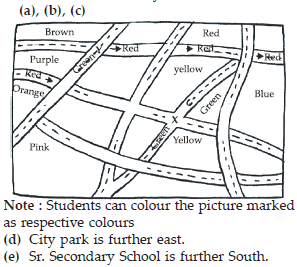
Look at the given map of a city.Answer the following.
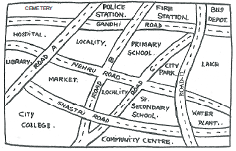
(a) Colour the map as follows : Blue-water, Red-fire station, Orange-library, Yellow-schools, Green-park, Pink-College, Purple-Hospital, Brown-Cemetery.
(b) Mark a green ‘X’ at the intersection of Road ‘C’ and Nehru Road, Green ‘Y’ at the intersection of Gandhi Road and Road A.
(c) In red, draw a short street route from Library to the bus depot.
(d) Which is further east, the city park or the market?
(e) Which is further south, the primary school or the Sr. Secondary School?
Draw a map of your class room using proper scale and symbols for different objects.
SOLUTION:Left for the students.
Q 7.Draw a map of your school compound using a proper scale and symbols for various features like play ground, main building, garden etc.
SOLUTION:Left for the students.
Q 8.Draw a map giving instructions to your friend so that she reaches your house without any difficulty.
SOLUTION:Left for the students.
Q 9.Can a polyhedron have for its faces
(i) 3 triangles?
(ii) 4 triangles?
(iii) a square and four triangles?
Since, we know that a polyhedron have greater than or equal to 4 faces.
(i) 3 triangles.
No
(ii) 4 triangles.
Yes, since it forms a triangular pyramid.
(iii) Yes, since it is a square pyramid.
Is it possible to have polyhedron with any given number of faces? (Hint : Think of a pyramid).
SOLUTION:Yes, it is possible, but only if the number of faces are greater than or equal to 4.
Q 11.Which are prisms among the following?
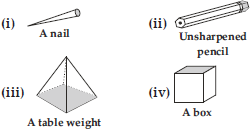
Since we know that a prism is a polyhedron, two of whose faces are congruent polygons in parallel planes and whose other faces are parallelograms. \ Only (ii) and (iv) are prisms.
Q 12.(i) How are prisms and cylinders alike?
(ii) How are pyramids and cones alike?
(i) A prism becomes a cylinder as the number of sides of its base becomes larger and larger.
(ii) A pyramid becomes a cone as the number of sides of its base becomes larger and larger.
Is a square prism same as a cube? Explain.
SOLUTION:No, because a square prism can be a cuboid also.
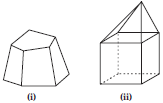
Q 14.Verify Euler’s formula for these solids.

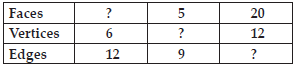
Using Euler’s formula find the unknown.

Can a polyhedron have 10 faces, 20 edges and 15 vertices?
SOLUTION: