Congruence of Triangles (Maths) Class 7 - NCERT Questions
Complete the following statements:
(A) Two line segments are congruent if ____________ .
(B) Among two congruent angles, one has a measure of 70°; the measure of the other angle is _______ .
(C) When we write ∠A = ∠B, we actually mean ________ .
(A) They have the same length.
(B) 70°
(C) m∠A = m∠B
Give any two real-life examples for congruent shapes
SOLUTION:(i) Sheets of same letter pad.
(ii) Biscuits in the same packet.
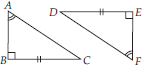
If ∆ABC ≅ ∆FED under the correspondence ABC ↔ FED, write all the corresponding congruent parts of the triangles.
SOLUTION: 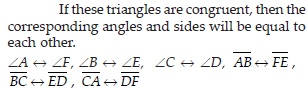
If DDEF ≅ ∆BCA, write the part(s) of ∆BCA that correspond to


Which congruence criterion do you use in the following?
(A) SSS, as all three sides of ∆ABC are equal to the corresponding sides of ∆DEF.
(B) SAS, as two sides and the angle included between these sides of ∆PQR are equal to the corresponding sides and included angle of ∆XYZ.
(C) ASA, as two angles and the side included between these angles of ∆LMN are equal to the corresponding angles and included side of ∆GFH.
(D) RHS, as in the given two right-angled triangles, one side and the hypotenuse are respectively equal.
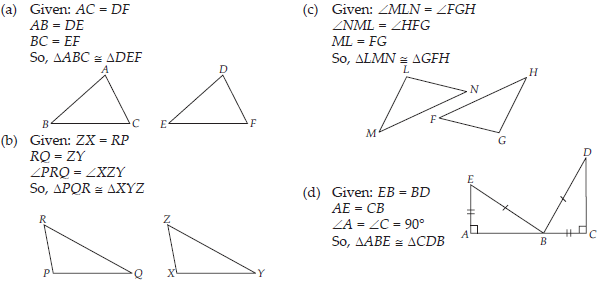
You want to show that ∆ART ≅ ∆PEN,
(A) If you have to use SSS criterion, then you need to show
(i) AR =
(ii) RT =
(iii) AT =
(B) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and (ii) PN =
(C) If it given that AT = PN and you are to use ASA criterion, you need to have
(i) ? (ii) ?
(A) (i) AR = PE (ii) RT = EN (iii) AT = PN
(B) (i) RT = EN (ii) PN = AT
(C) (i) ∠ATR = ∠PNE (ii) ∠RAT = ∠EPN
You have to show that ∆AMP ≅ ∆AMQ
In the following proof, supply the missing reasons.
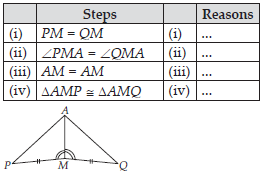
(i) Given
(ii) Given
(iii) Common
(iv) SAS, as the two sides and the angle included between these sides of ∆AMP are equal to corresponding sides and angle of ∆AMQ.
In ∆ABC, ∠A = 30°, ∠B = 40° and ∠C =110°
In ∆PQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ∆ABC ≅ ∆PQR by AAA congruence criterion. Is he justified? Why or why not?
No. This property represents that these triangles have their respective angles of equal measure.
However, this gives no information about their sides. The sides of these triangles have a ratio somewhat different from 1:1. Therefore, AAA property does not prove that the two triangles are congruent.
In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ∆RAT ≅ ?
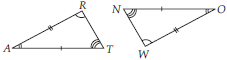
It can be observed that,
∠RAT = ∠WON
∠ART = ∠OWN
AR = OW
Therefore, ∆RAT ≅ ∆WON, by ASA criterion.
Complete the congruence statement:

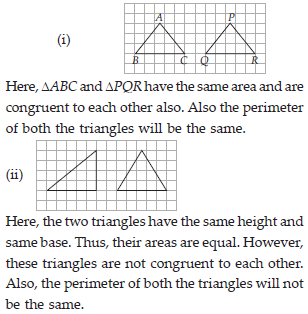
In a squared sheet, draw two triangles of equal areas such that
(i) the triangles are congruent.
(ii) the triangles are not congruent.
What can you say about their perimeters?
Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
SOLUTION: 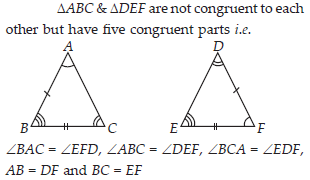
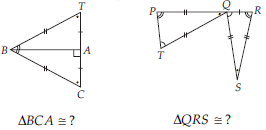
If ∆ABC and ∆PQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
SOLUTION: 
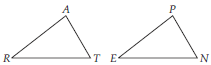
Explain, why ∆ABC ≅ ∆FED