Algebraic Expressions (Maths) Class 7 - NCERT Questions
Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.
(i) Subtraction of z from y.
(ii) One-half of the sum of numbers x and y.
(iii) The number z multiplied by itself.
(iv) One-fourth of the product of numbers p and q.
(v) Numbers x and y both squared and added.
(vi) Number 5 added to three times the product of numbers m and n.
(vii) Product of numbers y and z subtracted from 10.
(viii) Sum of numbers a and b subtracted from their product.
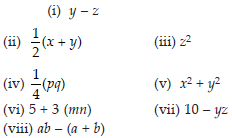
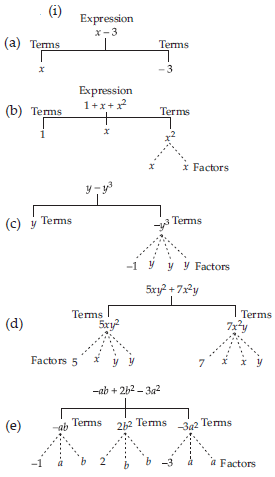
(i) Identify the terms and their factors in the following expressions show the terms and factors by tree diagrams.
(A) x – 3 (B) 1 + x + x2
(C) y – y3 (D) 5xy2 + 7x2y
(E) – ab + 2b2 – 3a2
(ii) Identify terms and factors in the
expressions given below :
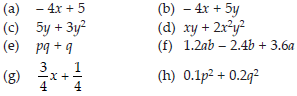
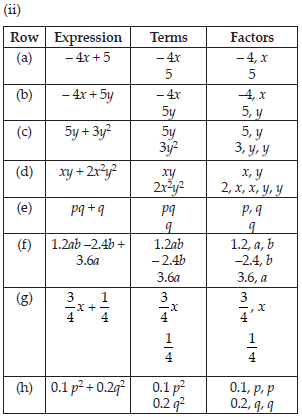
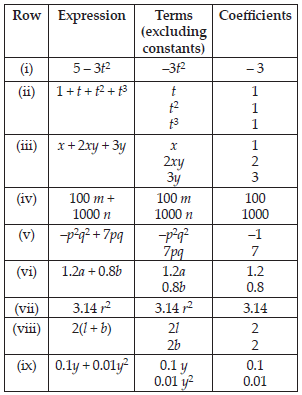
Identify the numerical coefficients of terms (other than constants) in the following expressions:
(i) 5 – 3t2
(ii) 1 + t + t2 + t3
(iii) x + 2xy + 3y
(iv) 100 m + 1000 n
(v) –p2q2 + 7pq
(vi) 1.2a + 0.8b
(vii) 3.14 r2
(viii) 2(l + b)
(ix) 0.1y + 0.01y2
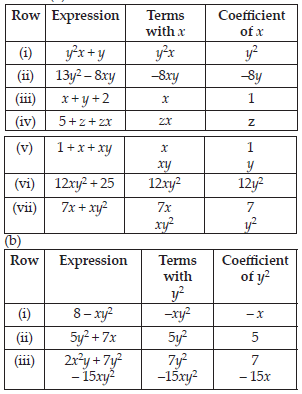
(A) Identify terms which contains x and give the coefficient of x.
(i) y2x + y (ii) 13y2 – 8xy
(iii) x + y + 2 (iv) 5 + z + zx
(v) 1 + x + xy (vi) 12xy2 + 25
(vii) 7x + xy2
(B) Identify terms which contains y2 and give the coefficient of y2.
(i) 8 – xy2 (ii) 5y2 + 7x
(iii) 2x2y – 15xy2 + 7y2
Classify into monomials, binomials and trinomials.
(i) 4y – 7z (ii) y2
(iii) x + y – xy (iv) 100
(v) ab – a – b (vi) 5 –3t
(vii) 4p2q –4pq2 (viii) 7mn
(ix) z2 – 3z + 8 (x) a2 + b2
(xi) z2 + z (xii) 1 + x + x2

State whether a given pair of terms is of like or unlike terms.
(i) 1, 100 (ii) −7x,5/2x,
(iii) –29x, – 29y (iv) 14xy, 42yx
(v) 4m2p, 4mp2 (vi) 12xz, 12x2z2
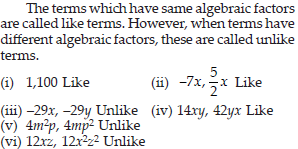
Identify like terms in the following:
(A) –xy2, –4yx2, 8x2, 2xy2, 7y, –11x2, –100x, –11yx, 20x2y, –6x2, y, 2xy, 3x
(B) 10pq, 7p, 8q, –p2q2, –7qp, – 100q, –23, 12q2p2, – 5p2, 41, 2405p, 78qp, 13p2q, qp2, 701p2
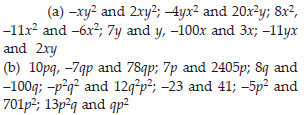
Simplify by combining like terms:
(i) 21b – 32 + 7b –20b
(ii) –z2 + 13z2 –5z + 7z2 – 15z
(iii) p – (p – q) –q –(q – p)
(iv) 3a – 2b – ab –(a – b + ab) + 3ab + b – a
(v) 5x2y – 5x2 + 3yx2 –3y2 + x2 – y2 + 8xy2 – 3y2
(vi) (3y2 + 5y – 4) – (8y – y2 – 4)
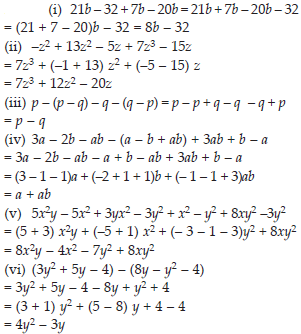
Add :
(i) 3mn, –5mn, 8mn, –4mn
(ii) t –8tz, 3tz – z, z – t
(iii) –7mn + 5, 12mn + 2, 9mn –8, –2mn – 3
(iv) a + b – 3, b – a + 3, a – b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy,
4xy
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
(vii) 4x2y, –3xy2, –5xy2, 5x2y
(viii)3p2q2 – 4pq + 5, –10p2q2, 15 + 9pq + 7p2q2
(ix) ab – 4a, 4b – ab, 4a – 4b
(x) x2 – y2 – 1, y2 – 1 – x2, 1 – x2 – y2
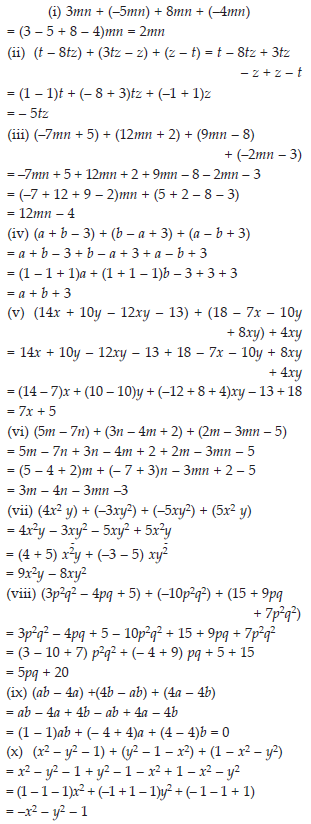
Subtract :
(i) –5y2 from y2
(ii) 6xy from –12xy
(iii) (a – b) from (a + b)
(iv) a(b – 5) from b (5 – a)
(v) – m2 + 5mn from 4m2 – 3mn + 8
(vi) – x2 + 10x – 5 from 5x – 10
(vii) 5a2 –7ab + 5b2 from 3ab – 2a2 – 2b2
(viii) 4pq – 5q2 – 3p2 from 5p2 + 3q2 – pq
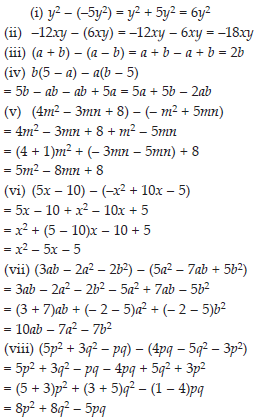
(A) What should be added to x2 + xy + y2 to obtain 2x2 + 3xy?
(B) What should be subtracted from 2a + 8b + 10 to get – 3a + 7b + 16?
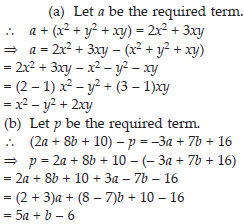
What should be taken away from 3x2 – 4y2 + 5xy + 20 to obtain – x2 – y2 + 6xy + 20 ?
SOLUTION: 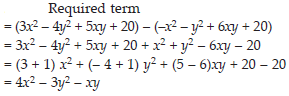
(A) From the sum of 3x – y + 11 and –y – 11, subtract 3x – y – 11.
(B) From the sum of 4 + 3x and 5 – 4x + 2x2, subtract the sum of 3x2 – 5x and –x2 + 2x + 5.
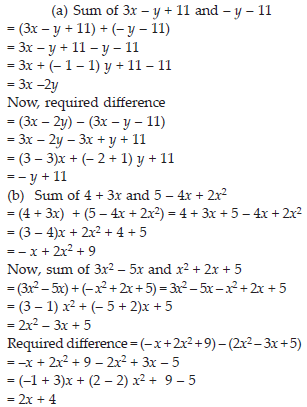
If m = 2, find the value of:
(i) m – 2 (ii) 3m – 5
(iii) 9 – 5m (iv) 3m2 – 2m – 7
(v) (5m/2)-4
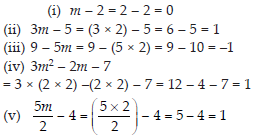
If p = –2, find the value of:
(i) 4p + 7 (ii) –3p2 + 4p + 7
(iii) –2p3 – 3p2 + 4p + 7
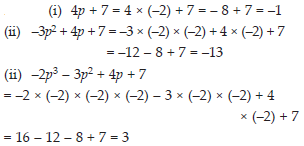
Find the value of the following expressions, when x = –1:
(i) 2x – 7 (ii) –x + 2
(iii) x2 + 2x + 1 (iv) 2x2 –x – 2
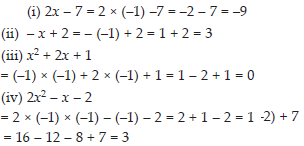
If a = 2, b = –2, then find the value of:
(i) a2 + b2 (ii) a2 + ab + b2
(iii) a2 – b2
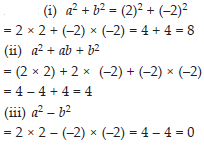
When a = 0, b = –1, find the value of the given expressions:
(i) 2a + 2b (ii) 2a2 + b2 + 1
(iii) 2a2b + 2ab2 + ab (iv) a2 + ab + 2
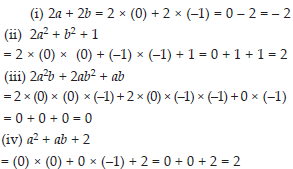
Simplify the expressions and find the value, if x is equal to 2
(i) x + 7 + 4 (x – 5)
(ii) 3(x + 2) + 5x – 7
(iii) 6x + 5(x –2)
(iv) 4(2x – 1) + 3x + 11
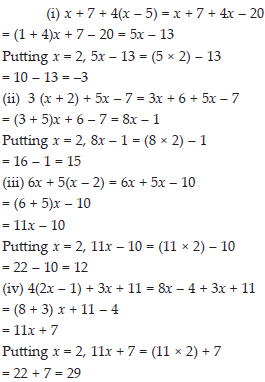
Simplify these expressions and find their values if x = 3, a = –1, b = –2.
(i) 3x – 5 – x + 9 (ii) 2 – 8x + 4x + 4
(iii) 3a + 5 – 8a + 1 (iv) 10 – 3b – 4 – 5b
(v) 2a – 2b – 4 – 5 + a
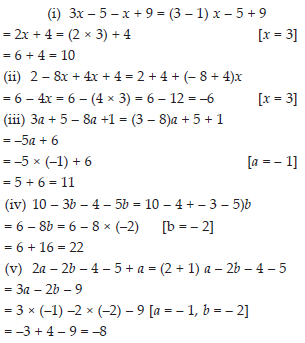
(i) If z = 10, find the value of z3 – 3(z – 10).
(ii) If p = –10, find the value of p2 – 2p –100.
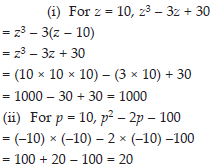
What should be the value of a if the value of 2x2 + x – a equals to 5, when x = 0?
SOLUTION: 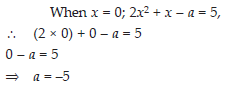
Simplify the expression 2(a2 + ab) + 3 – ab and find its value when a = 5 and b = –3.
SOLUTION: 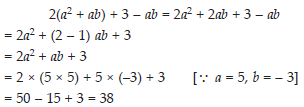
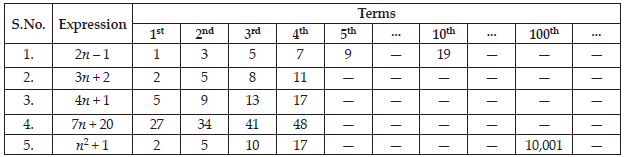
Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.


Use the given algebraic expression to complete the table of number patterns.