Mensturation (Mathematics) Class 6 - NCERT Questions
Find the perimeter of each of the following figures :
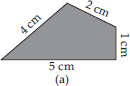
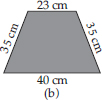
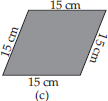
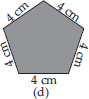
(A) Perimeter = Sum of all the sides
= 4 cm + 2 cm + 1 cm + 5 cm = 12 cm
(B) Perimeter = Sum of all the sides
= 23 cm + 35 cm + 40 cm + 35 cm = 133 cm
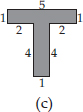
(C) Perimeter = Sum of all the sides
= 15 cm + 15 cm + 15 cm + 15 cm = 60 cm
(D) Perimeter = Sum of all the sides
= 4 cm + 4 cm + 4 cm + 4 cm + 4 cm = 20 cm
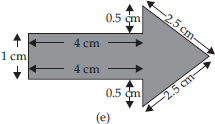
(E) Perimeter = Sum of all the sides
= 1 cm + 4 cm + 0.5 cm + 2.5 cm + 2.5 cm
+ 0.5 cm + 4 cm = 15 cm
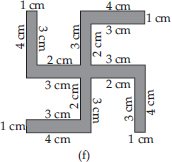
(F) Perimeter = Sum of all the sides
= 4 cm + 1 cm + 3 cm + 2 cm + 3 cm
+ 4 cm + 1 cm + 3 cm + 2 cm + 3 cm + 4 cm
+ 1 cm + 3 cm + 2 cm + 3 cm + 4 cm
+ 1 cm + 3 cm + 2 cm + 3 cm
= 52 cm
The lid of a rectangular box of sides 40 cm by 10 cm is sealed all round with tape. What is the length of the tape required?

Total length of tape required
= Perimeter of rectangle
= 2 × (length + breadth)
= 2 × (40 + 10) cm
= 2 × 50 cm = 100 cm = 1 m
Thus, the total length of tape required is 100 cm or 1 m.
A table-top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the table-top?
SOLUTION: Length of table-top = 2 m 25 cm = 2.25 m
Breadth of table-top = 1 m 50 cm = 1.50 m
Perimeter of table-top = 2 × (length + breadth)
= 2 × (2.25 + 1.50) m = 2 × 3.75 m = 7.50 m
Thus, perimeter of table-top is 7.5 m.
What is the length of the wooden strip required to frame a photograph of length and breadth
32 cm and 21 cm respectively?
Length of wooden strip
= Perimeter of photograph
= 2 × (length + breadth)
= 2 × (32 + 21) cm = 2 × 53 cm = 106 cm
Thus, the length of the wooden strip required is 106 cm.
A rectangular piece of land measures 0.7 km by 0.5 km. Each side is to be fenced with 4 rows of wires. What is the length of the wire needed?
SOLUTION: Since, 4 rows of wires are needed. Therefore, the total length of wire is equal to 4 times the perimeter of land.
Perimeter of land = 2 × (length + breadth)
= 2 × (0.7 + 0.5) km = (2 × 1.2) km = 2.4 km
= 2.4 × 1000 m = 2400 m
Thus, the length of wire
= 4 × 2400 m = 9600 m = 9.6 km
Find the perimeter of each of the following shapes :
(A)A triangle of sides 3 cm, 4 cm and 5 cm.
(B)An equilateral triangle of side 9 cm.
(C)An isosceles triangle with equal sides 8 cm each and third side 6 cm.
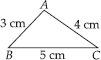
(A) Perimeter of ΔABC
= AB + BC + CA = 3 cm + 5 cm + 4 cm
= 12 cm
(B) Perimeter of equilateral ΔABC
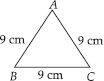
= 3 × side
= 3 × 9 cm
= 27 cm
(C) Perimeter of ΔABC
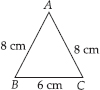
= AB + BC + CA
= 8 cm + 6 cm + 8 cm
= 22 cm
Find the perimeter of a triangle with sides measuring 10 cm, 14 cm and 15 cm.
SOLUTION: Perimeter of triangle
= Sum of all three sides
= 10 cm + 14 cm + 15 cm = 39 cm
Thus, perimeter of triangle is 39 cm.
Find the perimeter of a regular hexagon with each side measuring 8 m.
SOLUTION: Perimeter of regular hexagon
= 6 × length of one side = 6 × 8 m = 48 m
Thus, the perimeter of regular hexagon is 48 m.
Find the side of the square whose perimeter is 20 m.
SOLUTION: Perimeter of square = 4 × side
⇒ 20 m = 4 × side ⇒ side = 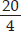 m = 5m
m = 5m
Thus, the side of square is 5 m.
The perimeter of a regular pentagon is 100 cm. How long is its each side?
SOLUTION: Perimeter of regular pentagon = 5 × side
⇒ 100 cm = 5 × side ⇒ side = 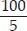 cm = 20 cm
cm = 20 cm
Thus, the side of regular pentagon is 20 cm.
A piece of string is 30 cm long. What will be the length of each side if the string is used to form:
(A) a square?
(B) an equilateral triangle?
(C) a regular hexagon?
Length of string = Perimeter of each shape
(A) Perimeter of square = 4 × side
⇒ 30 cm = 4 × side ⇒ side = 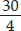 cm = 7.5 cm
cm = 7.5 cm
Thus, the length of each side of square will be 7.5 cm.
(B) Perimeter of equilateral triangle = 3 × side
⇒ 30 cm = 3 × side ⇒ side = 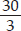 cm = 10 cm
cm = 10 cm
Thus, the length of each side of equilateral triangle will be 10 cm.
(C) Perimeter of regular hexagon = 6 × side
⇒ 30 cm = 6 × side ⇒ side = 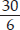 cm = 5 cm
cm = 5 cm
Thus, the length of each side of regular hexagon will be 5 cm.
Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
SOLUTION: Let the length of third side be x cm.
Length of other two sides are 12 cm and 14 cm.
Now, perimeter of triangle = 36 cm
⇒ 12 + 14 + x = 36 ⇒ 26 + x = 36
⇒ x = 36 - 26 ⇒ x = 10
Thus, the length of third side is 10 cm.
Find the cost of fencing a square park of side 250 m at the rate of Rs 20 per metre.
SOLUTION: Side of square park = 250 m
Perimeter of square park = 4 × side
= 4 × 250 m = 1000 m
Since, cost of fencing for 1 metre = Rs 20
Therefore, cost of fencing for 1000 metres
= Rs 20 × 1000 = Rs 20,000
Find the cost of fencing a rectangular park of length 175 m and breadth 125 m at the rate of
Rs 12 per metre.
Length of rectangular park = 175 m
Breadth of rectangular park = 125 m
Perimeter of park = 2 × (length + breadth)
= 2 × (175 + 125) m
= 2 × 300 m = 600 m
Since, cost of fencing park for 1 metre = Rs 12
Therefore, cost of fencing park for 600 m
= Rs 12 × 600 = Rs 7,200
Sweety runs around a square park of side 75 m. Bulbul runs around a rectangular park with length 60 m and breadth 45 m. Who covers less distance?
SOLUTION: Distance covered by Sweety
= Perimeter of square park = 4 × side
= 4 × 75 m = 300 m
Thus, distance covered by Sweety is 300 m.
Now, distance covered by Bulbul
= Perimeter of rectangular park
= 2 × (length + breadth)
= 2 × (60 + 45) m = 2 × 105 m = 210 m
Thus, Bulbul covers a distance of 210 m.
So, Bulbul covers less distance.
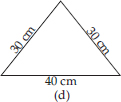
What is the perimeter of each of the following figures? What do you infer from the answers?
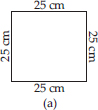

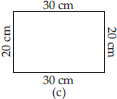
(A) Perimeter of square = 4 × side
= 4 × 25 cm = 100 cm
(B) Perimeter of rectangle
= 2 × (length + breadth)
= 2 × (40 + 10) cm = 2 × 50 cm = 100 cm
(C) Perimeter of rectangle = 2 × (length + breadth)
= 2 × (30 + 20) cm = 2 × 50 cm = 100 cm
(D) Perimeter of triangle = Sum of all sides
= 30 cm + 30 cm + 40 cm = 100 cm
Thus, all the figures have same perimeter.
Avneet buys 9 square paving slabs, each with a side of 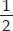 m. He lays them in the form of a square.
m. He lays them in the form of a square.
(A) What is the perimeter of his arrangement [see fig. (i)]?
(B) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement [see fig. (ii)]?
(C) Which has greater perimeter?
(D) Avneet wonders if there is a way of getting an even greater perimeter. Can you find a way of doing this? (The paving slabs must meet along complete edges i.e. they cannot be broken.)
(A) Side of one small square = 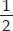 m
m
∴ Side of given square =  m
m
Perimeter of square = 4 × side
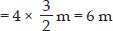
(B) Perimeter of given figure
= sum of all sides = 20 × 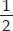 m = 10 m
m = 10 m
(C) The cross arrangement has greater perimeter.
(D) It is not possible to determine the arrangement with perimeter greater than 10 m.
Find the areas of the following figures by counting square :
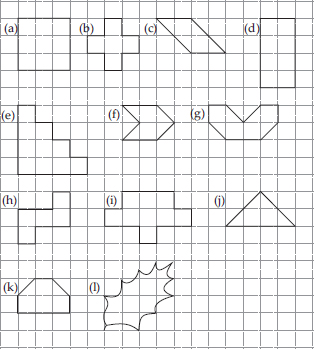
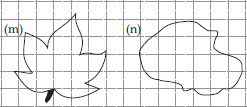
(A) Number of fully-filled squares = 9
∴ Area covered by fully-filled squares
= (9 × 1) sq. units = 9 sq. units
(B) Number of fully-filled squares = 5
∴ Area covered by fully-filled squares
= (5 × 1) sq. units = 5 sq. units
(C) Number of fully-filled squares = 2
Number of half-filled squares = 4
∴ Area covered by fully-filled squares
= (2 × 1) sq. units = 2 sq. units
Area covered by half-filled squares
= 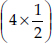 sq. units = 2 sq. units
sq. units = 2 sq. units
∴ Total area = (2 + 2) sq. units = 4 sq. units
(D) Number of fully-filled squares = 8
∴ Area covered by fully-filled squares
= (8 × 1) sq. units = 8 sq. units
(E) Number of fully-filled squares = 10
∴ Area covered by fully-filled squares
= (10 × 1) sq. units = 10 sq. units
(F) Number of fully-filled squares = 2
Number of half-filled squares = 4
∴ Area covered by fully-filled squares
= (2 × 1) sq. units = 2 sq. units
Area covered by half-filled squares
= 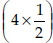 sq. units = 2 sq. units
sq. units = 2 sq. units
∴ Total area = (2 + 2) sq. units = 4 sq. units
(G) Number of fully-filled squares = 4
Number of half-filled squares = 4
∴ Area covered by fully-filled squares
= (4 × 1) sq. units = 4 sq. units
Area covered by half-filled squares
= 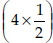 sq. units = 2 sq. units
sq. units = 2 sq. units
∴ Total area = (4 + 2) sq. units = 6 sq. units
(h) Number of fully-filled squares = 5
∴ Area covered by fully-filled squares
= (5 × 1) sq. units = 5 sq. units
(i) Number of fully-filled squares = 9
∴ Area covered by fully-filled squares
= (9 × 1) sq. units = 9 sq. units
(j) Number of fully-filled squares = 2
Number of half-filled squares = 4
∴ Area covered by fully-filled squares
= (2 × 1) sq. units = 2 sq. units
Area covered by half-filled squares
= 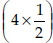 sq. units = 2 sq. units
sq. units = 2 sq. units
∴ Total area = (2 + 2) sq. units = 4 sq. units
(k) Number of fully-filled squares = 4
Number of half-filled squares = 2
∴ Area covered by fully-filled squares
= (4 × 1) sq. units = 4 sq. unit
Area covered by half-filled squares
= 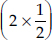 sq. units = 1 sq. units
sq. units = 1 sq. units
∴ Total area = (4 + 1) sq. units = 5 sq. units
(l) Number of fully-filled squares = 2,
Number of half-filled squares = 0,
Number of more than half-filled squares = 6
and number of less than half-filled squares = 6.
Now, estimated area covered by
fully-filled squares = 2 sq. units,
half filled squares = 0 sq. units
more than half-filled squares = 6 sq. units
and less than half-filled squares = 0 sq. unit
∴ Total area = (2 + 0 + 6 + 0) sq. units = 8 sq. units.
(m) Number of fully-filled squares = 5
Number of more than half-filled squares =9
and number of less than half-filled squares = 12
Estimated area covered by
fully-filled squares = 5 sq. units
more than half-filled squares = 9 sq. units
and less than half-filled squares = 0 sq. unit
∴ Total area = (5 + 9+ 0) sq. units = 14 sq. units
(n) Number of fully-filled squares = 8
Number of more than half-filled squares = 10
and number of less than half-filled squares = 9
Estimated area covered by
fully-filled squares = 8 sq. units,
more than half-filled squares = 10 sq. units
less than half-filled squares = 0 sq. unit
∴ Total area = (8 + 10 + 0) sq. units = 18 sq. units.
Find the areas of the rectangles whose sides are :
(A) 3 cm and 4 cm
(B) 12 m and 21 m
(C) 2 km and 3 km
(D) 2 m and 70 cm
(A) Area of rectangle = length × breadth
= 3 cm × 4 cm = 12 cm2
(B) Area of rectangle = length × breadth
= 12 m × 21 m = 252 m2
(C) Area of rectangle = length × breadth
= 2 km × 3 km = 6 km2
(D) Area of rectangle = length × breadth
= 2 m × 70 cm = 2 m × 0.7 m = 1.4 m2
Find the areas of the squares whose sides are:
(A) 10 cm
(B) 14 cm
(C) 5 m
(A) Area of square = side × side
= 10 cm × 10 cm = 100 cm2
(B) Area of square = side × side
= 14 cm × 14 cm = 196 cm2
(C) Area of square = side × side
= 5 m × 5 m = 25 m2
The length and breadth of three rectangles are as given below :
(A) 9 m and 6 m
(B) 17 m and 3 m
(C) 4 m and 14 m
Which one has the largest area and which one has the smallest?
(A) Area of rectangle = length × breadth
= 9 m × 6 m = 54 m2
(B) Area of rectangle = length × breadth
= 17 m × 3 m = 51 m2
(C) Area of rectangle = length × breadth
= 4 m × 14 m = 56 m2
Thus, rectangle (C) has the largest area, i.e. 56 m2 and rectangle (B) has the smallest area, i.e., 51 m2.
The area of a rectangular garden 50 m long is
300 sq m. Find the width of the garden.
Length of rectangle = 50 m
Area of rectangle = 300 m2
Since, area of rectangle = length × breadth
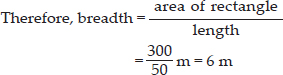
Thus, the breadth of the garden is 6 m.
What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of
Rs 8 per hundred sq. m?
Length of land = 500 m
breadth of land = 200 m
Area of land = length × breadth
= 500 m × 200 m = 1,00,000 sq. m
Cost of tiling 100 sq. m of land = Rs 8
∴ Cost of tiling 1,00,000 sq. m of land
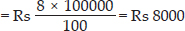
A table-top measures 2 m by 1 m 50 cm. What is its area in square metres?
SOLUTION: Length of table-top = 2 m
Breadth of table-top = 1 m 50 cm = 1.50 m
∴ Area of table-top = length × breadth
= 2 m × 1.50 m = 3 m2
A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?
SOLUTION: Length of room = 4 m
And breadth of room = 3 m 50 cm = 3.50 m
∴ Area of carpet = length × breadth
= 4 m × 3.50 m = 14 m2
A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
SOLUTION: Length of floor = 5 m
and breadth of floor = 4 m
Area of floor = length × breadth = 5 m × 4 m = 20 m2
Now, side of square carpet = 3 m
Area of square carpet = side × side = 3 m × 3 m = 9 m2
∴ Area of floor that is not carpeted
= 20 m2 - 9 m2 = 11 m2
Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
SOLUTION: Side of square flower bed = 1 m
Area of square flower bed = side × side
= 1 m × 1 m = 1 m2
∴ Area of 5 square flower beds = (1 × 5) m2 = 5 m2
Now, length of land = 5 m
And breadth of land = 4 m
Area of land = length × breadth = 5 m × 4 m = 20 m2
∴ Area of remaining part
= Area of land - Area of 5 flower beds
= 20 m2 - 5 m2 = 15 m2
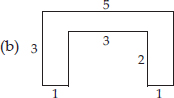
By splitting the following figures into rectangles, find their areas (The measures are given in centimetres).
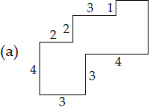
(A) We have,
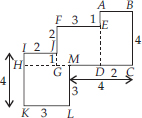
Area of square HKLM = (3 × 3) cm2 = 9 cm2
Area of rectangle IJGH = (1 × 2) cm2 = 2 cm2
Area of square FEDG = (3 × 3) cm2 = 9 cm2
Area of rectangle ABCD = (2 × 4) cm2 = 8 cm2
∴ Total area of the figure
= (9 + 2 + 9 + 8) cm2 = 28 cm2
(B) We have,
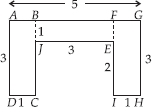
Area of rectangle ABCD = (3 × 1) cm2 = 3 cm2
Area of rectangle BJEF = (3 × 1) cm2 = 3 cm2
Area of rectangle FGHI = (3 × 1) cm2 = 3 cm2
∴ Total area of the figure = (3 + 3 + 3) cm2 = 9 cm2
Split the following shapes into rectangles and find their areas. (The measures are given in centimetres).
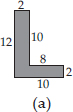
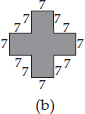
(A) We have,
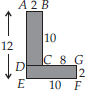
Area of rectangle ABCD = (2 × 10) cm2 = 20 cm2
Area of rectangle DEFG = (10 × 2) cm2 = 20 cm2
∴ Total area of the figure = (20 + 20) cm2 = 40 cm2
(B) We have,
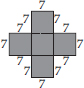
There are 5 squares each of side 7 cm.
Area of one square = (7 × 7) cm2 = 49 cm2
∴ Area of 5 squares = (5 × 49) cm2 = 245 cm2
(C) We have,
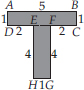
Area of rectangle ABCD = (5 × 1) cm2 = 5 cm2
Area of rectangle EFGH = (4 × 1) cm2 = 4 cm2
∴ Total area of the figure = (5 + 4) cm2 = 9 cm2
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively:
(A) 100 cm and 144 cm
(B) 70 cm and 36 cm.
(A) Area of rectangular region
= length × breadth = 100 cm × 144 cm = 14400 cm2
Area of one tile = 12 cm × 5 cm = 60 cm2
∴ Number of tiles

Thus, 240 tiles are required.
(B) Area of rectangular region
= length × breadth = 70 cm × 36 cm = 2520 cm2
Area of one tile = 12 cm × 5 cm = 60 cm2
∴ Number of tiles
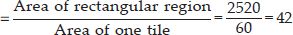
Thus, 42 tiles are required.