Co-ordinate Geometry - NCERT Questions
Find the distance between the following pairs of points :
(i) (2, 3), (4, 1)
(ii) (-5, 7), (-1, 3)
(iii) (a, b)(-a, -b)
Soln. : (i) Here x1 = 2, y1 = 3 and x2 = 4 and y2 = 1
∴ The required distance
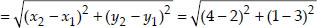
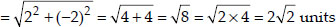
(ii) Here x1 = -5, y1 = 7 and x2 = -1, y2 = 3
∴ The required distance
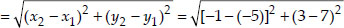
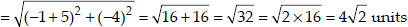
(iii) Here x1 = a, y1 = b and x2 = -a, y2 = -b
∴ The required distance
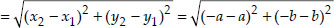
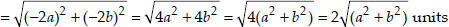
Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed below as following : 'Atown B is located 36 km east and 15 km North of the town A'.
SOLUTION:
Soln. : Part-I
Let the points be A(0, 0) and B(36, 15)
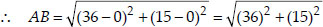
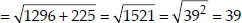
Part-II
We have A(0, 0) and B(36, 15) as the positions of two towns
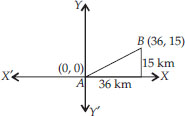
Here x1 = 0, x2 = 36 and y1 = 0, y2 = 15
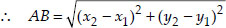
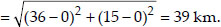 .
.
Determine if the points (1, 5), (2, 3) and
(-2, -11) are collinear.
Soln. : Let the points be A(1, 5), B(2, 3) and
C(-2, -11) A, B and C are collinear, if
AB + BC = AC, AC + CB = AB, BA + AC = BC
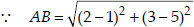
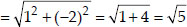
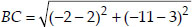
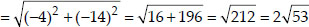
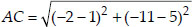
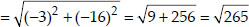
But AB + BC ≠ AC, AC + CB ≠ AB, BA + AC ≠ BC
∴ A, B and C are not collinear.
Check whether (5, -2), (6, 4) and (7,-2) are the vertices of an isosceles triangle.
SOLUTION:
Soln. : Let the points be A(5, -2), B(6, 4) and C(7, -2).
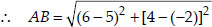
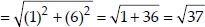

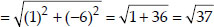
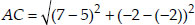
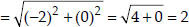
We have AB = BC ≠ AC.
∴ ∆ABC is an isosceles triangle.
In a classroom, 4 friends are seated at the point A, B, C and D as shown in figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, "Don't you think ABCD is a square?" Chameli disagrees. Using distance formula, find which of them is correct.
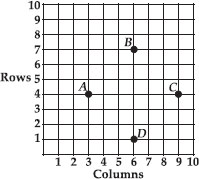
Soln. : Let the number of horizontal columns represent the x-coordinates whereas the vertical rows represent the y-coordinates.
∴ The points are : A(3, 4), B(6, 7), C(9, 4) and D(6, 1)

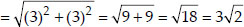

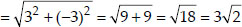
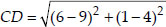
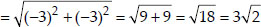
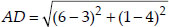
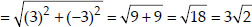
Since, AB = BC = CD = AD i.e., All the four sides are equal.
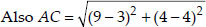
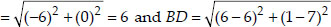
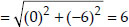
i.e., BD = AC ⇒ Both the diagonals are also equal.
∴ ABCD is a square.
Thus, Champa is correct.
Name the type of quadrilateral formed if any, by the following points, and give reasons for your answer :
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
(ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Soln. : (i) Let the points be A(-1, -2), B(1, 0),
C(-1, 2) and D(-3, 0) of a quadrilateral ABCD.
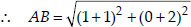
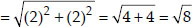
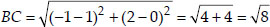
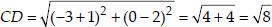
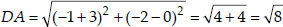
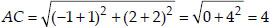

⇒ AB = BC = CD = AD i.e., All the sides are equal. And AC = BD
Also, AC and BD (the diagonals) are equal.
∴ ABCD is a square.
(ii) Let the points be A(-3, 5), B(3, 1), C(0, 3) and D(-1, -4).
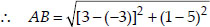
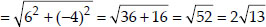
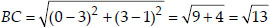
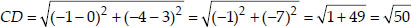
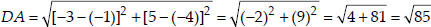
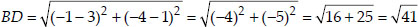
We see that 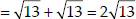
i.e., AC + BC = AB
⇒ A, B and C are collinear. Thus, ABCD is not a quadrilateral.
(iii) Let the points be A(4, 5), B(7, 6), C(4, 3) and D(1, 2).
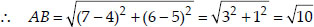
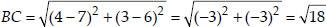
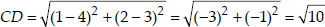
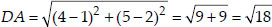

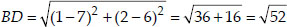
Since, AB = CD, BC = DA [opposite sides of the quadrilateral are equal]
And AC ≠ BD ⇒ Diagonals are unequal.
∴ ABCD is a parallelogram.
Find the point on the x-axis which is equidistant from (2, -5) and (-2, 9).
SOLUTION:
Soln. : We know that any point on x-axis has its ordinate = 0.
Let the required point be P(x, 0).
Let the given points be A(2, -5) and B(-2, 9)
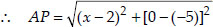
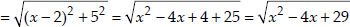
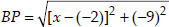
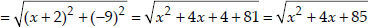
Since, A and B are equidistant from P,
∴ AP = BP
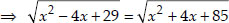
⇒ x2 - 4x + 29 = x2 + 4x + 85
⇒ x2 - 4x - x2 - 4x = 85 - 29
⇒ -8x = 56 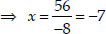
∴ The required point is (-7, 0)
Find the values of y for which the distance between the points P(2, -3) and Q(10, y) is 10 units.
SOLUTION:
Soln. : The given points are P(2, -3) and Q(10, y).
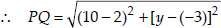
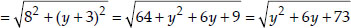
But PQ = 10

Squaring both sides, y2 + 6y + 73 = 100
⇒ y2 + 6y - 27 = 0
⇒ y2 - 3y + 9y - 27 = 0
⇒ (y - 3)(y + 9) = 0
⇒ Either y - 3 = 0 ⇒ y = 3
or y + 9 = 0 ⇒ y = -9
∴ The required value of y is 3 or -9.
If Q(0, 1) is equidistant from P(5, -3) and
R(x, 6), find the values of x. Also find the distances QR and PR.
Soln. : 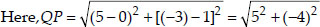
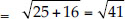
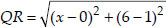
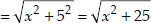
∴ QP = QR
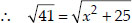
Squaring both sides, we have x2 + 25 = 41
⇒ x2 + 25 - 41 = 0
⇒ x2 - 16 = 0 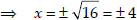
Thus, the point R is (4, 6) or (-4, 6)
Now,
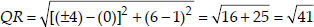
and 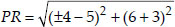
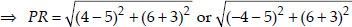
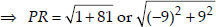
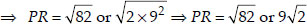
Find a relation between x and y such that the point (x, y) is equidistant from the point
(3, 6) and (-3, 4).
Soln. : Let the points be A(x, y), B(3, 6) and C(-3, 4).

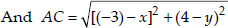
Since, the point (x, y) is equidistant from (3, 6) and (-3, 4).
∴ AB = AC
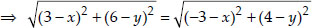
Squaring both sides,
(3 - x)2 + (6 - y)2 = (-3 - x)2 + (4 - y)2
⇒ (9 + x2 - 6x) + (36 + y2 - 12y)
= (9 + x2 + 6x) + (16 + y2 - 8y)
⇒ 9 + x2 - 6x + 36 + y2 - 12y - 9 - x2 - 6x
- 16 - y2 + 8y = 0
⇒ - 6x - 6x + 36 - 12y - 16 + 8y = 0
⇒ - 12x - 4y + 20 = 0
⇒ - 3x - y + 5 = 0
⇒ 3x + y - 5 = 0 which is the required relation between x and y.
Find the coordinates of the point which divides the join of (-1, 7) and (4, -3) in the ratio 2 : 3.
SOLUTION:
Soln. : Let the required point be P(x, y).
Here the end points are (-1, 7) and (4, - 3)
∴ Ratio = 2 : 3 = m1 : m2
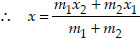
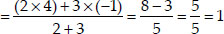
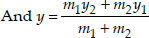
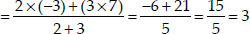
Thus, the required point is (1, 3).
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
SOLUTION:
Soln. : Let the given points be A(4, -1) and B(-2, -3).

Let the points P and Q trisect AB.
i.e., AP = PQ = QB
i.e., P divides AB in the ratio of 1 : 2
Q divides AB in the ratio of 2 : 1
Let the coordinates of P be (x, y)
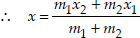
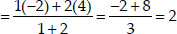
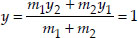
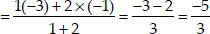
∴ The required co-ordinates of P are 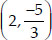
Let the co-ordinates of Q be (X, Y)
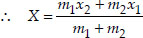
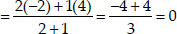
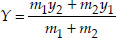
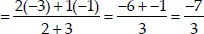
∴ The required coordinates of Q are 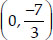
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in the figure. Niharika runs 1/4th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly half way between the line segment joining the two flags, where should she post her flag ?.
SOLUTION:
Soln. : Let us consider 'A' as origin, then
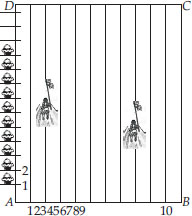
AB is the x-axis.
AD is the y-axis.
Now, the position of green flag-post is 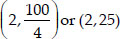
And, the position of red flag-post is 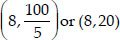
⇒ Distance between both the flags
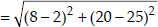
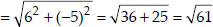
Let the mid-point of the line segment joining the two flags be M(x, y).
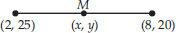
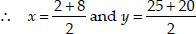
or x = 5 and y = 22.5
Thus, the blue flag is on the 5th line at a distance 22.5 m above AB.
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by
(-1, 6).
Soln. : Let the given points are A(-3, 10) and
B(6, -8).
Let the point P(-1, 6) divides AB in the ratio m1 : m2.
∴ Using the section formula, we have
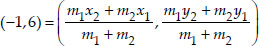
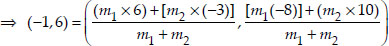
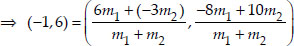
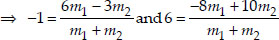
⇒ -1(m1 + m2) = 6m1 - 3m2
and 6(m1 + m2) = - 8m1 + 10m2
⇒ -m1 - m2 - 6m1 + 3m2 = 0
and 6m1 + 6m2 + 8m1 - 10m2 = 0
⇒ -7m1 + 2m2 = 0
and 14m1 - 4m2 = 0 or 7m1 - 2m2 = 0
⇒ 2m2 = 7m1 and 7m1 = 2m2
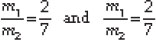
⇒ m1 : m2 = 2 : 7 and m1 : m2 = 2 : 7
Thus, the required ratio is 2 : 7.
Find the ratio in which the line segment joining A(1, -5) and B(-4, 5) is divided by the x-axis. Also find the coordinates of the point of division.
SOLUTION:
Soln. : The given points are : A(1, -5) and B(-4, 5).
Let the required ratio = k : 1 and the required point be P(x, y)
Part-I : To find the ratio
Since the point P lies on x-axis,
∴ Its y-coordinate is 0.
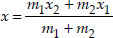 and 0
and 0 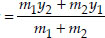
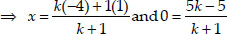
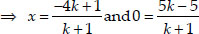
⇒ x(k + 1) = - 4k + 1
and 5k - 5 = 0 ⇒ k = 1
⇒ x(k + 1) = - 4k + 1
⇒ x(1 + 1) = - 4 + 1 [∴ k = 1]
⇒ 2x = -3
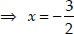
∴ The required ratio k : 1 = 1 : 1
Coordinates of P are (x, 0) 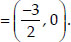
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
SOLUTION:
Soln. : The given points are : A(1, 2), B(4, y),
C(x, 6) and D(3, 5)
Since, the diagonals of a parallelogram bisect each other.
∴ The coordinates of P are :
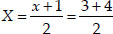
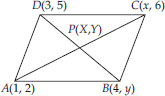
⇒ x + 1 = 7 ⇒ x = 6
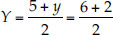
⇒ 5 + y = 8 ⇒ y = 3
∴ The required values of x and y are : x = 6, y = 3.
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4)
SOLUTION:
Soln. : Here, centre of the circle is O(2, -3)
Let the end points of the diameter be A(x, y) and B(1, 4)
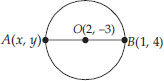
The centre of a circle bisects the diameter.
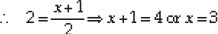
And 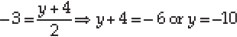
Here the coordinates of A are (3, -10)
If A and B are (-2, -2) and (2, -4) respectively, find the coordinates of P such that AP = 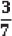 AB and P lies on the line segment AB.
AB and P lies on the line segment AB.
Soln. : 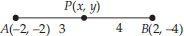
Here the given points are A(-2, -2) and B(2, -4)
Let the coordinates of P are (x, y)
Since, the point P divides AB such that
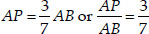
⇒ AB = AP + BP
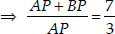
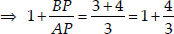
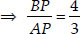
⇒ AP : PB = 3 : 4 i.e., P(x, y) divides AB in the ratio 3 : 4.
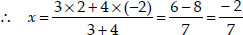
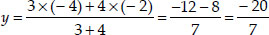
Thus, the coordinates of P are 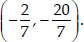
Find the coordinates of the points which divide the line segment joining A(-2, 2) and B(2, 8) into four equal parts.
SOLUTION:
Soln. : Here the given points are A(-2, 2) and
B(2, 8)
Let P1, P2 and P3 divide AB in four equal parts.
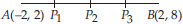
AP1 = P1P2 = P2P3 = P3B
Obviously, P2 is the mid-point of AB
∴ Coordinates of P2 are
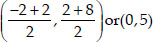
Again, P1 is the mid-point of AP2.
∴ Coordinates of P1 are
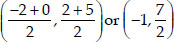
Also P3 is the mid-point of P2B.
∴ Coordinates of P3 are
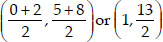
Thus, the coordinates of P1, P2 and P3 are 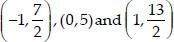 respectively.
respectively.
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2, -1) taken in order.
[Hint : Area of a rhombus =  (product of its diagonals)]
(product of its diagonals)]
Soln. : Let the vertices of the given rhombus are : A(3, 0), (4, 5), (-1, 4) and (-2, -1)
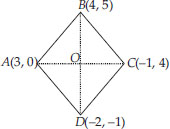
∴ AC and BD are the diagonals of rhombus ABCD.
∴ Diagonal
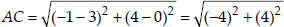
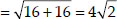
Diagonal 
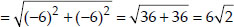
∴ For a rhombus,
Area 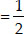 × (Product of diagonals)
× (Product of diagonals)
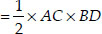
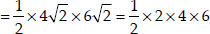
= 4 × 6 = 24 square units.
Find the area of the triangle whose vertices are :
(i) (2, 3), (-1, 0), (2, -4)
(ii) (-5, -1), (3, -5), (5, 2)
Soln. : (i) Let the vertices of the triangles be A(2, 3), B(-1, 0) and C(2, - 4)
Here x1 = 2, y1 = 3,
x2 = -1, y2 = 0
x3 = 2, y3 = -4
∴ Area of a ∆
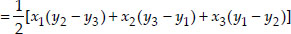
∴ Area of a ∆ABC
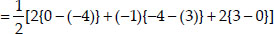
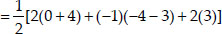
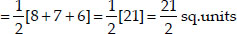
(ii) Let the vertices of the triangles be
A(-5, -1), B(3, -5) and C(5, 2)
i.e., x1 = -5, y1 = -1
x2 = 3, y2 = -5
x3 = 5, y3 = 2
∵ Area of a
∆ 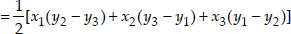
∴ Area of a ∆ABC
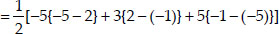
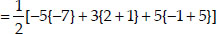
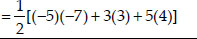
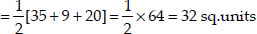
In each of the following find the value of 'k', for which the points are collinear.
(i) (7, -2), (5, 1), (3, k)
(ii) (8, 1), (k, -4), (2, -5)
Soln. : The given three points will be collinear if the ∆ formed by them has equal to zero area.
(i) Let A(7, -2), B(5, 1) and C(3, k) be the vertices of a triangle.
∴ The given points will be collinear, if
ar (∆ABC) = 0
or 7(1 - k) + 5(k + 2) + 3(-2 - 1) = 0
⇒ 7 - 7k + 5k + 10 + (-6) - 3 = 0
⇒ 17 - 9 + 5k - 7k = 0
⇒ 8 - 2k = 0 ⇒ 2k = 8 ⇒ 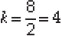
The required value of k = 4.
(ii) 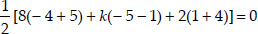
⇒ 8 - 6k + 10 = 0 ⇒ 6k = 18 ⇒ k = 3.
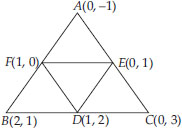
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the given triangle.
SOLUTION:
Soln. : Let the vertices of the triangle be A(0, -1), B(2, 1) and C(0, 3).
Let D, E and F be the mid-points of the sides BC, CA and AB respectively. Then :
Coordinates of D are
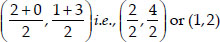
Coordinates of E are 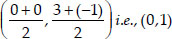
Coordinates of F are 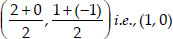
Now, ar(∆ABC)
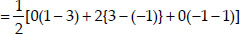
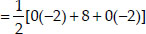
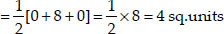
Now, ar(∆DEF) 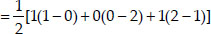
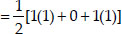
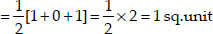
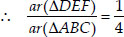
∴ ar(∆DEF) : ar(∆ABC) = 1 : 4.
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
SOLUTION:
Soln. : Let A(- 4, - 2), B(- 3, - 5), C(3, - 2) and
D(2, 3) be the vertices of the quadrilateral.
Let us join diagonal BD.
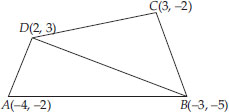
Now, ar(∆ABD)
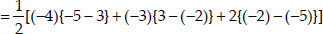
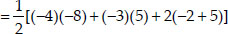
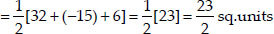
Now, ar(∆CBD)
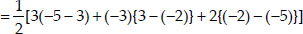
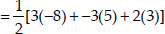
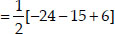
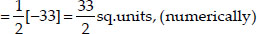
Since, ar(quad ABCD) = ar(∆ABD) + ar∆CBD
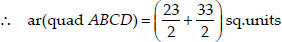
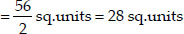
You have studied in class IX that a median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ABC whose vertices are A(4, -6), B(3, -2) and C(5, 2).
SOLUTION:
Soln. : Here, the vertices of the triangles are A(4, -6), B(3, -2) and C(5, 2).
Let D be the midpoint of BC.
∴ The coordinates of the mid point D are
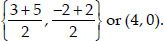
Since AD divides the triangle ABC into two parts i.e., ∆ABD and ∆ACD,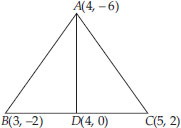
Now, ar(∆ABD)
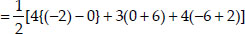
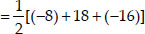
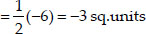
= 3 sq.units (numerically) ........ (1)
ar(∆ADC)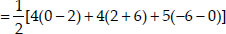
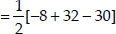
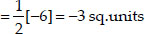
= 3 sq.units (numerically) ........ (1)
From (1) and (2)
ar(∆ABD) = ar(∆ADC)
i.e., A median divides the triangle into two triangles of equal areas.
Determine the ratio in which the line 2x + y - 4 = 0 divides the line segment joining the points
A(2, -2) and B(3, 7).
Soln. : Let the required ratio be k : 1 and the point C divide them in the above ratio.
∴ Coordinates of C are 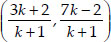
Since the point C lies on the given line
2x + y - 4 = 0,
∴ We have 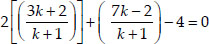
⇒ 2(3k + 2) + (7k - 2) = 4 × (k + 1)
⇒ 6k + 4 + 7k - 4k - 4 - 2 = 0
⇒ (6 + 7 - 4)k + (-2) = 0 ⇒ 9k - 2 = 0
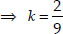
∴ The required ratio = k : 1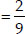
Find a relation between x and y if the points
(x, y), (1, 2) and (7, 0) are collinear.
Soln. : The given points are A(x, y), B(1, 2) and
C(7, 0) are collinear
The points A, B and C will be collinear if area of
∆ABC = 0 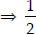 [x(2 - 0) + 1 (0 - y) + 7(y - 2) = 0
[x(2 - 0) + 1 (0 - y) + 7(y - 2) = 0
or if 2x - y + 7y - 14 = 0
or if 2x + 6y - 14 = 0 or if x + 3y - 7 = 0 which is the required relation between x and y.
Find the centre of circle passing through the points (6, -6), (3, -7) and (3, 3)
SOLUTION:
Soln. : Let P(x, y) be the centre of the circle since the circle is passing through
A(6, -6), B(3, -7) and C(3, 3)
∴ AP = BP = CP
Taking AP = BP, we have AP2 = BP2
⇒ (x - 6)2 + (y + 6)2 = (x - 3)2 + (y + 7)2
⇒ x2 - 12x + 36 + y2 + 12y + 36
= x2 - 6x + 9 + y2 + 14y + 49
⇒ - 12x + 6x + 12y - 14y + 72 - 58 = 0
⇒ - 6x - 2y + 14 = 0
⇒ 3x + y - 7 = 0 ..... (1) [Dividing by (-2)]
Taking BP = CP, we have BP2 = CP2
⇒ (x - 3)2 + (y + 7)2 = (x - 3)2 + (y - 3)2
⇒ x2 - 6x + 9 + y2 + 14y + 49
= x2 - 6x + 9 + y2 - 6y + 9
⇒ - 6x + 6x + 14y + 6y + 58 - 18 = 0
⇒ 20y + 40 = 0
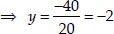 ........ (2)
........ (2)
From (1) and (2),
3x - 2 - 7 = 0
⇒ 3x = 9 ⇒ x = 3
i.e., x = 3 and y = -2
∴ The required centre is (3, -2).
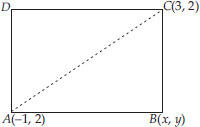
The two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of the other two vertices.
SOLUTION:
Soln. : Let us have a square ABCD such that A(-1, 2) and C(3, 2) are the opposite vertices.
Let B(x, y) be an unknown vertex.
Since all sides of a square are equal,
∴ AB = BC ⇒ AB2 = BC2
⇒ (x + 1)2 + (y - 2)2 = (x - 3)2 + (y - 2)2
⇒ 2x + 1 = -6x + 9
⇒ 8x = 8 ⇒ x = 1 ........ (1)
Since each angle of a square = 90°,
∴ ABC is a right angled triangle.
∴ Using Pythagoras theorem, we have :
AB2 + BC2 = AC2
⇒ [(x + 1)2 + (y - 2)2] + [(x - 3)2 + (y - 2)2]
= [(3 + 1)2 + (2 - 2)2]
⇒ 2x2 + 2y2 + 2x - 4y - 6x - 4y + 1 + 4 + 9 + 4 = 16
⇒ 2x2 + 2y2 - 4x - 8y + 2 = 0
⇒ x2 + y2 - 2x - 4y + 1 = 0 ........ (2)
Substituting the value of x from (1) into (2) we have
1 + y2 - 2 - 4y + 1 = 0
⇒ y2 - 4y + 2 - 2 = 0
⇒ y2 - 4y = 0 ⇒ y(y - 4) = 0
⇒ y = 0 or y = 4
Hence, the two required other vertices are
(1, 0) and (1, 4).
The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.
(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinats of the vertices of ∆PQR if C is the origin ?
Also calculate the areas of the triangles in these cases. What do you observe ?
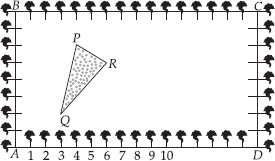
Soln. : (i) By taking A as the origin and AD and AB as the coordinate axes. We have P(4, 6), Q(3, 2) and R(6, 5) as the vertices of ∆PQR.
(ii) By taking C as the origin and CB and CD as the coordinate axes, then the vertices of ∆PQR are P(- 12, - 2), Q(- 13, - 6) and R(- 10, - 3)
Now ar(∆PQR) [when P(4, 6), Q(3, 2) and
R(6, 5) are the vertices]
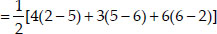 sq. units
sq. units
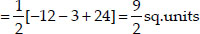
[taking numerical value]
ar(∆PQR) [when P(-12, -2), Q(-13, -6) and R(-10, -3) are the vertices]
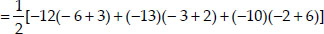
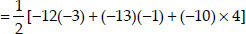
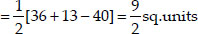
Thus, in both cases, the area of ∆PQR is the same.
The vertices of a ∆ABC are A(4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides
AB and AC at D and E respectively, such that 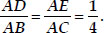 Calculate the area of the ∆ADE and compare it with the area of ∆ABC. [Recall "The converse of basis proportionality theorem", and "theorem of similar triangles taking their areas and corresponding sides"]
Calculate the area of the ∆ADE and compare it with the area of ∆ABC. [Recall "The converse of basis proportionality theorem", and "theorem of similar triangles taking their areas and corresponding sides"]
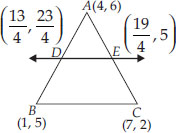
Soln. : We have 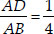
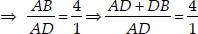
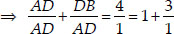
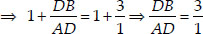
⇒ AD : DB = 1 : 3
Thus, the point D divides AB in the ratio
1 : 3
∴ The coordinates of D are :
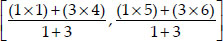
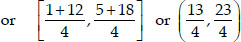
Similarly, AE : EC = 1 : 3 i.e., E divides AC in the ratio 1 : 3
⇒ Coordinates of E are
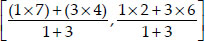
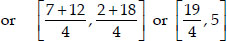
Now, ar(∆ADE)
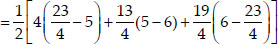
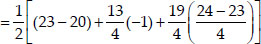
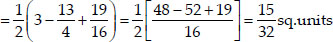
Area of ∆ABC 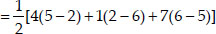
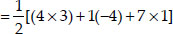
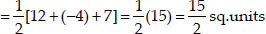
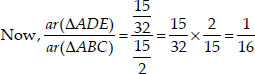
⇒ ar(∆ADE) : ar(∆ABC) = 1 : 16.
Let A(4, 2), B(6, 5) and C(1, 4) be the vertices of ∆ABC.
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
(iii) Find the coordinates of points Q and R on medians BE and CF respectively such that
BQ : QE = 2 : 1 and CR : RF = 2 : 1
(iv) What do you observe ?
[Note : The point which is common to all the three medians is called the centroid and this point divides each median in the ratio 2 : 1.]
(v) If A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC, find the coordinates of the centroid of the triangle.
Soln. : We have the vertices of ∆ABC as A(4, 2),
B(6, 5) and C(1, 4).
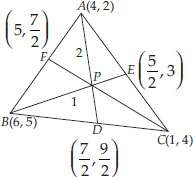
(i) Since AD is a median
∴ Coordinates of D are
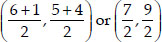
(ii) Since AP : PD = 2 : 1 i.e., P divides AD in the ratio 2 : 1
∴ Coordinates of P are
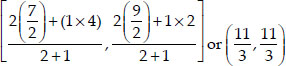
(iii) BQ : QE = 2 : 1 ⇒ [The point Q divides BE in the ratio 2 : 1]
[coordinates of E are 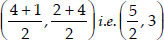
∴ Coordinates of Q are
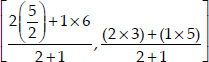
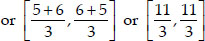
Also, CR : RF = 2 : 1
⇒ The point R divides CF in the ratio 2 : 1
∴ Coordinates of F are 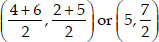
So, Coordinates of R are
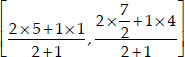
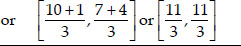
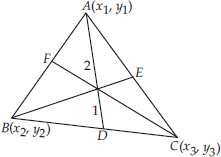
(iv) We observe that P, Q and R represent the same point.
(v) Here, we have A(x1, y1), B(x2, y2) and
C(x3, y3) are the vertices of ∆ABC. Also AD, BE and CE are its medians.
∴ D, E and F are the mid points of BC, CA and AB respectively.
We know, the centroid is a point on a median, dividing it in the ratio 2 : 1.
Considering the median AD, coordinates of
D are 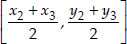
Let G be the centroid.
∴ Coordinates of the centroid are
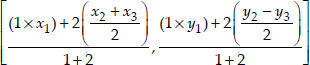
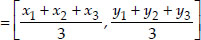
Similarly, considering the other medians we find that in each the coordinates of G are
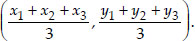
i.e., The coordinates of the centroid are
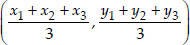
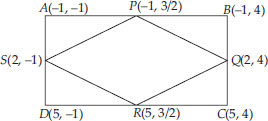
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the mid points of AB, BC, CD and DA respectively. Is the quadrilateral PQRS is square? a rectangle? or a rhombus? Justify your answer.
SOLUTION:
Soln. : We have a rectangle whose vertices are
A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1).
∵ P is mid-point of AB
∴ Coordinates of P are
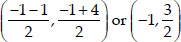
Similarly, Coordinates of Q are
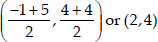
Coordinates of R are 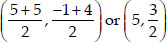
Coordinates of S are 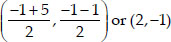
Now, 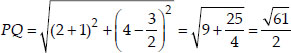
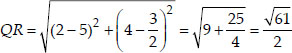
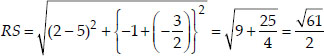
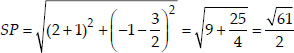
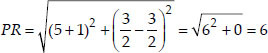
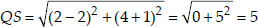
We see that PQ = QR = RS = SP i.e., all sides of PQRS are equal.
∴ It can be a square or a rhombus.
But its diagonals are not equal.
i.e., PR ≠ QS
∴ PQRS is a rhombus.