Quadratic Equations - NCERT Questions
Check whether the following are quadratic equations:
(i) (x + 1)2 = 2(x - 3)
(ii) x2 - 2x = (-2)(3 - x)
(iii) (x - 2)(x + 1) = (x - 1)(x + 3)
(iv) (x - 3)(2x + 1) = x(x + 5)
(v) (2x - 1)(x - 3) = (x + 5)(x - 1)
(vi) x2 + 3x + 1 = (x - 2)2
(vii) (x + 2)3 = 2x(x2 - 1)
(viii) x3 - 4x2 - x + 1 = (x - 2)3
Soln. : (i) x2 + 2x + 1 = 2x - 6
⇒ x2 + 2x + 1 - 2x + 6 = 0
⇒ x2 + 7 = 0
Since x2 + 7 is a quadratic polynomial.
∴ (x + 1)2 = 2(x - 3) is a quadratic equation.
(ii) x2 - 2x = - 6 + 2x ⇒ x2 - 2x - 2x + 6 = 0
⇒ x2 - 4x + 6 = 0
Since x2 - 4x + 6 is a quadratic polynomial
∴ x2 - 2x = (-2)(3 - x) is a quadratic equation.
(iii) x2 - x - 2 = x2 + 2x - 3
⇒ x2 - x - 2 - x2 - 2x + 3 = 0
⇒ - 3x + 1 = 0
Since - 3x + 1 is a linear polynomial.
∴ (x - 2)(x + 1) = (x - 1)(x + 3) is not a quadratic equation.
(iv) 2x2 + x - 6x - 3 = x2 + 5x
⇒ 2x2 - 5x - 3 - x2 - 5x = 0 ⇒ x2 - 10x - 3 = 0
Since x2 - 10x - 3 is a quadratic polynomial.
∴ (x - 3)(2x + 1) = x(x + 5) is a quadratic equation.
(v) 2x2 - 6x - x + 3 = x2 - x + 5x - 5
⇒ 2x2 - x2 - 6x - x + x - 5x + 3 + 5 = 0
⇒ x2 - 11x + 8 = 0
Since x2 - 11x + 8 is a quadratic polynomial
∴ (2x - 1)(x - 3) = (x + 5)(x - 1) is a quadratic equation.
(vi) x2 + 3x + 1 = x2 - 4x + 4
⇒ x2 + 3x + 1 - x2 + 4x - 4 = 0 ⇒ 7x - 3 = 0
Since 7x - 3 is a linear polynomial.
∴ x2 + 3x + 1 = (x - 2)2 is not a quadratic equation.
(vii) x3 + 3x2(2) + 3x(2)2 + (2)3 = 2x3 - 2x
⇒ x3 + 6x2 + 12x + 8 = 2x3 - 2x
⇒ x3 + 6x2 + 12x + 8 - 2x3 + 2x = 0
⇒ -x3 + 6x2 + 14x + 8 = 0
Since -x3 + 6x2 + 14x + 8 is a polynomial of degree 3
∴ (x + 2)3 = 2x(x2 - 1) is not a quadratic equation.
(viii) x3 - 4x2 - x + 1 = x3 + 3x2(-2) + 3x(-2)2 + (-2)3
⇒ x3 - 4x2 - x + 1 = x3 - 6x2 + 12x - 8
⇒ x3 - 4x2 - x + 1 - x3 + 6x2 - 12x + 8 = 0
⇒ 2x2 - 13x + 9 = 0
Since 2x2 - 13x + 9 is a quadratic polynomial.
∴ x3 - 4x2 - x + 1 = (x - 2)3 is a quadratic equation.
Represent the following situations in the form of quadratic equations
(i) The area of a rectangular plot is 528 m2. The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
(ii) The product of two consecutive positive integers is 306. We need to find the integers.
(iii) Rohan's mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan's present age.
(iv) A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/hr less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
Soln. : (i) Let the breadth = x metres
∴ Length = 2(Breadth) + 1
∴ Length = (2x + 1)metres
Since Length × Breadth = Area
∴ (2x + 1) × x = 528 ⇒ 2x2 + x = 528
⇒ 2x2 + x - 528 = 0
Thus, the required quadratic equation is
2x2 + x - 528 = 0
(ii) Let the two consecutive positive integers be x and (x + 1)
∴ Product of the positive integers = 306
∴ x(x + 1) = 306 ⇒ x2 + x = 306
⇒ x2 + x - 306 = 0
Thus, the required quadratic equation is
x2 + x - 306 = 0
(iii) Let the present age of Rohan be x years
∴ Mother's age = (x + 26) years
After 3 years, Rohan's age = (x + 3) years.
Mother's age = [(x + 26) + 3] years = (x + 29) years
According to the condition, [Product of their ages after 3 years] = 360
⇒ (x + 3) × (x + 29) = 360
⇒ x2 + 29x + 3x + 87 = 360
⇒ x2 + 29x + 3x + 87 - 360 = 0
⇒ x2 + 32x - 273 = 0
Thus, the required quadratic equation is
x2 + 32x - 273 = 0.
(iv) Let the speed of the train = u km/hr
Distance covered = 480 km
Time taken = Distance ÷ Speed
= (480 ÷ u) hours
In second case, Speed = (u - 8) km/hour
∴ 
According to the condition, 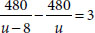
⇒ 480u - 480(u - 8) = 3u(u - 8)
⇒ 480u - 480u + 3840 = 3u2 - 24u
⇒ 3840 - 3u2 + 24u = 0 ⇒ u2 - 8u - 1280 = 0
Thus, the required quadratic equation is
u2 - 8u - 1280 = 0.
Find the roots of the following quadratic equations by factorisation
(i) x2 - 3x - 10 = 0 (ii) 2x2 + x - 6 = 0
(iii) 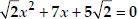
(iv) 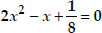
(v) 100x2 - 20x + 1 = 0
Soln. : (i) We have, x2 - 3x - 10 = 0,
x2 - 5x + 2x - 10 = 0
⇒ x(x - 5) + 2(x - 5) = 0 ⇒ (x - 5)(x + 2) = 0
Either x - 5 = 0 ⇒ x = 5 or x + 2 = 0 ⇒ x = -2
Thus, the required roots are x = 5 and x = -2
(ii) We have, 2x2 + x - 6 = 0
⇒ 2x2 + 4x - 3x - 6 = 0
⇒ 2x(x + 2) - 3(x + 2) = 0
⇒ (x + 2)(2x - 3) = 0
Either x + 2 = 0
⇒ x = -2 or 2x - 3 = 0 ⇒ 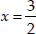
Thus, the required roots are x = -2 and 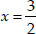
(iii) We have 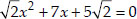
⇒ 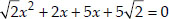
⇒ 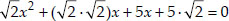
⇒ 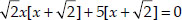
⇒ 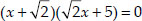
Either 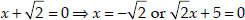
⇒ 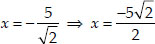
Thus, the required roots are
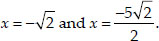
(iv) We have, 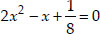
⇒ 16x2 - 8x + 1 = 0 ⇒ 16x2 - 4x - 4x + 1 = 0
⇒ 4x(4x - 1) - 1(4x - 1) = 0
⇒ (4x - 1)(4x - 1) = 0
⇒ 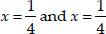
Thus, the required roots are 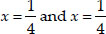
(v) We have, 100x2 - 20x + 1 = 0
⇒ 100x2 - 10x - 10x + 1 = 0
⇒ 10x(10x - 1) - 1(10x - 1) = 0
⇒ (10x - 1)(10x - 1) = 0
⇒ (10x - 1) = 0 and (10x - 1) = 0
⇒ 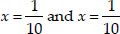
Thus, the required roots are 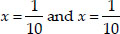
Solve the problems :
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was 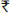 750. We would like to find out the number of toys produced on that day.
750. We would like to find out the number of toys produced on that day.
Soln. : (i) Let John had x marbles and the Jivanti had (45 - x).
When both of them lost 5 marbles then equation becomes
∴ (x - 5) × (45 - x - 5) = 124
We have : x2 - 45x + 324 = 0
⇒ x2 - 9x - 36x + 324 = 0
⇒ x(x - 9) - 36(x - 9) = 0
⇒ (x - 9)(x - 36) = 0
Either x - 9 = 0 ⇒ x = 9 or x - 36 = 0 ⇒ x = 36
Thus, x = 9 and x = 36
∴ John has 9 marbles and Jivanti had
45 - 9 = 36 marbles
(ii) Let the number of toys produced on that day be x.
Then cost of 1 toy 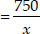
⇒ 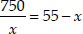 ⇒ x2 - 55x = -750
⇒ x2 - 55x = -750
⇒ x2 - 55x + 750 = 0
We have : x2 - 55x + 750 = 0
[∴ (-30) × (-25) = 750 and (-30) + (-25) = -55]
⇒ x2 - 30x - 25x + 750 = 0
⇒ x(x - 30) - 25(x - 30) = 0
⇒ (x - 30)(x - 25) = 0
Either x - 30 = 0 ⇒ x = 30
or x - 25 = 0 ⇒ x = 25
Thus, x = 30 and x = 25.
Find two numbers whose sum is 27 and product is 182.
SOLUTION:
Soln. : Here, sum of the numbers is 27.
Let one of the numbers be x.
∴ Other number = 27 - x
According to the condition, Product of the numbers = 182
⇒ x(27 - x) = 182 ⇒ 27x - x2 = 182
⇒ x2 - 27x + 182 = 0
⇒ x2 - 13x - 14x + 182 = 0
⇒ x(x - 13) - 14(x - 13) = 0
⇒ (x - 13)(x - 14) = 0
Either x - 13 = 0 ⇒ x = 13
or x - 14 = 0 ⇒ x = 14
Thus, the required numbers are 13 and 14.
Find two consecutive positive integers, sum of whose squares is 365.
SOLUTION:
Soln. : Let the two consecutive positive integers be x and (x + 1)
Since the sum of the square of the numbers
= 365
∴ x2 + (x + 1)2 = 365
⇒ x2 + [x2 + 2x + 1] = 365
⇒ x2 + x2 + 2x + 1 = 365
⇒ 2x2 + 2x + 1 - 365 = 0
⇒ 2x2 + 2x - 364 = 0 ⇒ x2 + x - 182 = 0
⇒ x2 + 14x - 13x - 182 = 0
⇒ x(x + 14) - 13(x + 14) = 0
⇒ (x + 14)(x - 13) = 0
Either x + 14 = 0 ⇒ x = -14 or x - 13 = 0
⇒ x = 13
Since x has to be a positive integer
⇒ x = -14 is rejected.
∴ x = 13 ⇒ x + 1 = 13 + 1 = 14
Thus, the required consecutive positive integers are 13 and 14.
The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
SOLUTION:Soln. : Let the base of the given right triangle be 'x' cm
∴ Its height = (x - 7) cm
∴ 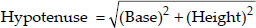
[By Pythagoras theorem]
∴ 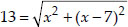
Squaring both sides, we get 169 = x2 + (x - 7)2
⇒ 169 = x2 + x2 - 14x + 49
⇒ 2x2 - 14x + 49 - 169 = 0
⇒ 2x2 - 14x - 120 = 0
⇒ x2 - 7x - 60 = 0 ⇒ x2 - 12x + 5x - 60 = 0
⇒ x(x - 12) + 5(x - 12) = 0
⇒ (x - 12)(x + 5) = 0
Either x - 12 = 0 ⇒ x = 12
or x + 5 = 0 ⇒ x = -5
But the sides of a triangle can never be negative ⇒ x = -5 is rejected.
⇒ x = 12
∴ Length of the base = 12 cm
⇒ Length of the height = (12 - 7)cm = 5 cm
Thus, the required base = 12 cm and
height = 5 cm.
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was  90, find the number of articles produced and the cost of each article.
90, find the number of articles produced and the cost of each article.
Soln. : Let the number of articles produced in a day = x
∴ Cost of production of each article
= 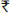 (2x + 3)
(2x + 3)
According to the condition, Total cost = 90
⇒ x × (2x + 3) = 90 ⇒ 2x2 + 3x = 90
⇒ 2x2 + 3x - 90 = 0 ⇒ 2x2 - 12x + 15x - 90 = 0
⇒ 2x(x - 6) + 15(x - 6) = 0
⇒ (x - 6)(2x + 15) = 0
Either x - 6 = 0 ⇒ x = 6
or 2x + 15 = 0 ⇒ 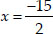
But the number of articles produced can never be negative,
∴ 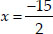 is rejected ⇒ x = 6
is rejected ⇒ x = 6
∴ Cost of each article = 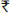 (2 × 6 + 3) =
(2 × 6 + 3) = 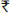 15
15
Thus, the required number of articles produced is 6 and the cost of each article is 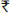 15.
15.
Find the roots of the following quadratic equations, if they exist, by the method of completing the square :
(i) 2x2 - 7x + 3 = 0 (ii) 2x2 + x - 4 = 0
(iii) 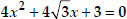
(iv) 2x2 + x + 4 = 0
Soln. : (i) We have, 2x2 - 7x + 3 = 0
Dividing throughout by the co-efficient of x2, we get 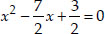
⇒ 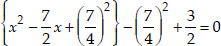
⇒ 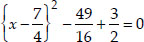
⇒ 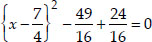
⇒ 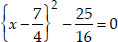
⇒ 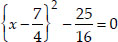
⇒ 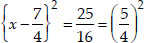
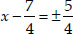
Case I : When  is positive,
is positive,
then 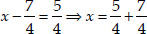
⇒ 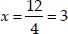
Case II : When  is negative,
is negative,
then 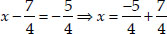 ⇒
⇒ 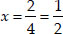
Thus, required roots are x = 3, and 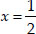
(ii) We have, 2x2 + x - 4 = 0
Dividing throughout by 2, 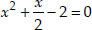
⇒ 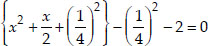
⇒ 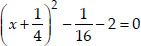
⇒ 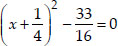
⇒ 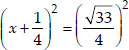
⇒ 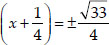
Case I : When 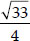 is positive,
is positive,
then 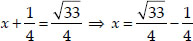
⇒ 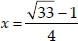
Case II : When 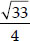 is negative,
is negative,
then 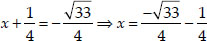
⇒ 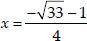
Thus, the required roots are
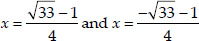
(iii) We have 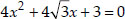
Dividing throughout by 4, we have
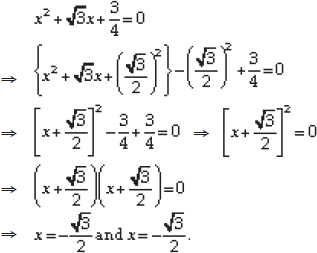
Dividing throughout by 2, we have 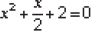
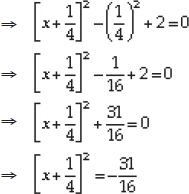
But the square of a number cannot be negative.
∴ 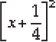 cannot give a real value.
cannot give a real value.
⇒ There is no real value of x satisfy the given equation.
Find the roots of the following quadratic equations, using the quadratic formula :
(i) 2x2 - 7x + 3 = 0 (ii) 2x2 + x - 4 = 0
(iii) 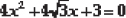 (iv) 2x2 + x + 4 = 0
(iv) 2x2 + x + 4 = 0
Soln. : (i) Comparing the given equation with
ax2 + bx + c = 0, we have
a = 2, b = -7, c = 3
∴ b2 - 4ac = (-7)2 - 4(2)(3) = 49 - 24 = 25 ≥ 0
Since b2 - 4ac > 0
∴ The given equation has real roots. The roots 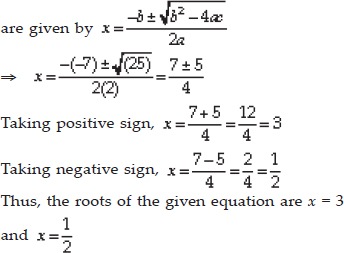
(ii) Comparing the given equation with
ax2 + bx + c = 0 we have a = 2, b = 1, c = - 4
∴ b2 - 4ac = (1)2 - 4(2)(-4) = 1 + 32 = 33 > 0
Since b2 - 4ac > 0
∴ The given equation has real roots. The roots 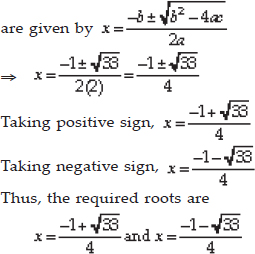
(iii) Comparing the given equation with
ax2 + bx + c = 0, we have a = 4, b =  , c = 3
, c = 3
∴ b2 - 4ac = ( )2 - 4(4)(3)
)2 - 4(4)(3)
= [16 × 3] - 48 = 48 - 48 = 0
Since b2 - 4ac = 0
∴ The given equation has real and equal roots, which are given by 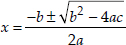
⇒ 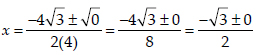
∴ 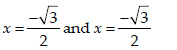
(iv) Comparing the given equation with
ax2 + bx + c = 0, we have a = 2, b = 1, c = 4
∴ b2 - 4ac = (1)2 - 4(2)(4) = 1 - 32 = -31 < 0
Since b2 - 4ac is less than 0, therefore the given equation does not have real roots.
Find the roots of the following equations :
(i) 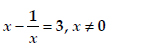
(ii) 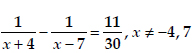
Soln. : (i) Here, we have :
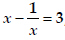
⇒ x2 - 1 = -3x ⇒ x2 - 3x - 1 = 0 …(1)
Comparing (1) with ax2 + bx + c = 0,
we have a = 1, b = -3, c = -1
∴ b2 - 4ac = (-3)2 - 4(1)(-1) = 9 + 4 = 13 > 0
∴ 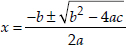
⇒ 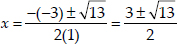
Now, taking positive sign, 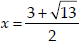
Now, taking negative sign, 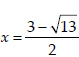
Thus, the required roots of the given equation are 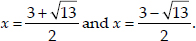
(ii) We have 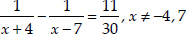
⇒ 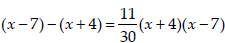
⇒ 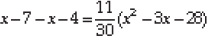
⇒ -11 × 30 = 11(x2 - 3x - 28)
⇒ - 30 = x2 - 3x - 28
⇒ x2 - 3x - 28 + 30 = 0
⇒ x2 - 3x + 2 = 0 …(1)
Comparing (1) with ax2 + bx + c = 0,
we have a = 1, b = -3, c = 2
∴ b2 - 4ac = (-3)2 - 4(1)(2) = 9 - 8 = 1 > 0
∴ The given equation (1) has real roots, which are given by 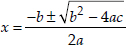
⇒ 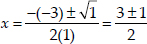
Taking positive sign, 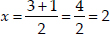
Taking negative sign, 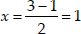
Thus, the required roots are x = 2 and x = 1.
The sum of the reciprocals of Rehman's ages, (in years) 3 years ago and 5 years from now is 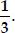 Find his present age.
Find his present age.
Soln. : Let the present age of Rehman = x
∴ 3 years ago Rehman's age = (x - 3) years
5 years later Rehman's age = (x + 5) years
Now, according to the condition,
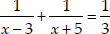
⇒ 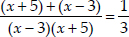
⇒ 3[x + 5 + x - 3] = (x - 3)(x + 5)
⇒ 3[2x + 2] = x2 + 2x - 15
⇒ 6x + 6 = x2 + 2x - 15
⇒ x2 + 2x - 6x - 15 - 6 = 0
⇒ x2 - 4x - 21 = 0 …(1)
Now, comparing (1) with ax2 + bx + c = 0, we have a = 1, b = -4, c = -21
∴ b2 - 4ac = (-4)2 - 4(1)(-21) = 16 + 84 = 100
Since, 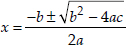
⇒ 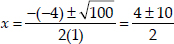
Taking positive sign,
we have 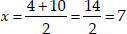
Taking negative sign,
we have 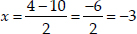
Since age cannot be negative,
∴ x ≠ -3 ⇒ x = 7
So, the present age of Rehman = 7 years.
In a class test, the sum of Shefali's marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
SOLUTION:
Soln. : Let Shefali's marks in Mathematics = x
∴ Marks in English = (30 - x)
[∴ Sum of the marks in English and Mathematics = 30]
Now, according to the condition
(x + 2) × [(30 - x) - 3] = 210
⇒ (x + 2) × (30 - x - 3) = 210
⇒ (x + 2)(- x + 27) = 210
⇒ -x2 + 25x + 54 = 210
⇒ -x2 + 25x + 54 - 210 = 0
⇒ -x2 + 25x - 156 = 0
⇒ x2 - 25x + 156 = 0 …(1)
Now, comparing (1) with ax2 + bx + c = 0, we have a = 1, b = -25, c = 156
∴ b2 - 4ac = (-25)2 - 4(1)(156) = 625 - 624 = 1
Since, 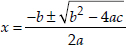
⇒ 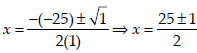
Taking positive sign, 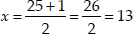
Taking negative sign, 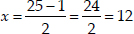
When x = 13, then 30 - 13 = 17
When x = 12, then 30 - 12 = 18
Thus, marks in Mathematics = 13, marks in English = 17
marks in Mathematics = 12,
marks in English = 18.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
SOLUTION:
Soln. : Let the shorter side (i.e., breadth) = x metres
∴ The longer side (length) = (x + 30) metres
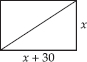
In a rectangle,

⇒ 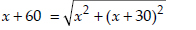
⇒ 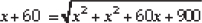
⇒ (x + 60)2 = 2x2 + 60x + 900
⇒ x2 + 120x + 3600 = 2x2 + 60x + 900
⇒ 2x2 - x2 + 60x - 120x + 900 - 3600 = 0
⇒ x2 - 60x - 2700 = 0 …(1)
Comparing (1) with ax2 + bx + c = 0, we have
a = 1, b = -60, c = -2700
∴ b2 - 4ac = (-60)2 - 4(1)(-2700)
⇒ b2 - 4ac = 3600 + 10800
⇒ b2 - 4ac = 14400
Since, 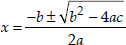
⇒ 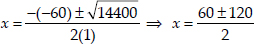
Taking +ve sign, 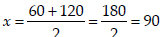
Taking -ve sign, 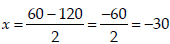
Since breadth cannot be negative,
so, x ≠ -30 ⇒ x = 90
∴ x + 30 = 90 + 30 = 120
Thus, the shorter side = 90 m. The longer side = 120 m.
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
SOLUTION:
Soln. : Let the larger number be x.
Since, (smaller number)2 = 8(larger number)
⇒ (smaller number)2 = 8x
⇒ smaller number = 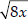
Now, according to the condition,
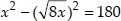
⇒ x2 - 8x = 180 ⇒ x2 - 8x - 180 = 0
Comparing (1) with ax2 + bx + c = 0, we have
a = 1, b = -8, c = -180
∴ b2 - 4ac = (-8)2 - 4(1)(-180) = 64 + 720 = 784
Since, 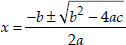
∴ 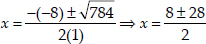 [∴
[∴ 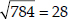 ]
]
Taking positive sign, 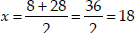
Taking negative sign, 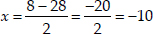
But x = -10 is not admissible,
∴ The larger number = 18
⇒ Smaller number =  =
= 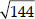 = ±12
= ±12
Thus, the smaller number = 12 or -12
Thus, the two numbers are 18 and 12, 18 and -12.
A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Find the speed of the train.
SOLUTION:Soln. : Let the uniform speed of the train be x km/hr
Since, time taken by the train 
⇒ 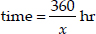
When speed is 5 km/hr more, then time taken is 1 hour less.
⇒ 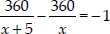 ⇒
⇒ 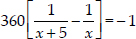
⇒ 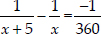 ⇒
⇒ 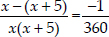
⇒ 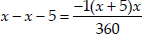
⇒ - 5 × 360 = -1(x2 + 5x)
⇒ - 5 × 360 = -x2 - 5x
⇒ x2 + 5x - 1800 = 0 …(1)
Comparing (1) with ax2 + bx + c = 0, we have
a = 1, b = 5, c = -1800
∴ b2 - 4ac = (5)2 - 4(1)(-1800)
= 25 + 7200 = 7225
Since, 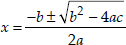
∴ 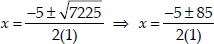
Taking positive sign, 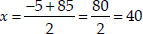
Taking negative sign, 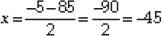
Since, the speed of a vehicle cannot be negative,
So, x = - 45 (rejected)
Thus, x = 40 ⇒ speed of the train = 40 km/hr.
Two water taps together can fill a tank in 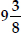 hours. The tap of larger diameter takes
hours. The tap of larger diameter takes
10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Soln. : Let the smaller tap fills the tank in x hours
∴ The larger tap fills the tank in (x - 10) hours.
Amount of water flowing through both taps in one hour
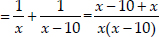
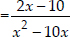
Now, according to the condition,
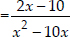
⇒ 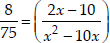 ⇒
⇒ 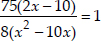
⇒ 8x2 - 80x = 150x - 750
⇒ 8x2 - 80x - 150x + 750 = 0
⇒ 8x2 - 230x + 750 = 0 …(1)
Comparing (1) with ax2 + bx + c = 0, we get
a = 8, b = -230, c = 750
∴ b2 - 4ac = (-230)2 - 4(8)750
= 52900 - 24000 = 28900 > 0
Since, 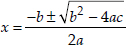
⇒ 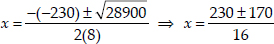
[∴ 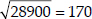 ]
]
Taking positive sign, 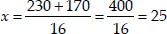
Taking negative sign, 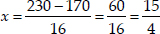
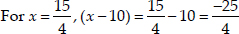
which is not possible.
[∴ Time cannot be negative]
∴ x = 25 ⇒ x - 10 = 25 - 10 = 15
Thus, time to fill the tank by the smaller tap alone = 25 hours and by larger tap alone = 15 hours.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/hr more than that of the passenger train, find the average speed of the two trains.
SOLUTION:
Soln. : Let the average speed of the passenger train be x km/hr
∴ Average speed of the express train
= (x + 11) km/hr
Total distance covered = 132 km
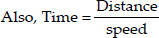
Time taken by the passenger train 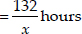
Time taken by the express train 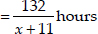
According to the condition,
we get 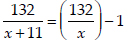
⇒ 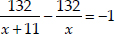 ⇒
⇒ 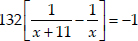
⇒ 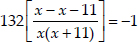 ⇒
⇒ 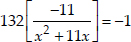
⇒ -11(132) = -1(x2 + 11x)
⇒ -1452 = -1(x2 + 11x)
⇒ x2 + 11x - 1452 = 0 …(1)
Comparing (1) with ax2 + bx + c = 0,
we get a = 1, b = 11, c = -1452
∴ b2 - 4ac = (11)2 - 4(1)(-1452)
⇒ b2 - 4ac = 121 + 5808 = 5929
Since, 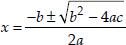
⇒ 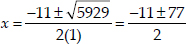
∴ Taking +ve sign, 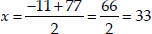
Taking -ve sign, 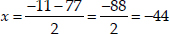
But average speed cannot be negative so,
x ≠ -44 ∴ x = 33
⇒ Average speed of the passenger train
= 33 km/hr
∴ Average speed of the express train
= (x + 11) km/hr = (33 + 11) km/hr = 44 km/hr
Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, find the sides of the two squares.
SOLUTION:
Soln. : Let the side of the smaller square be x m
⇒ Perimeter of the smaller square = 4x m
∴ Perimeter of the larger square = (4x + 24) m
⇒ side of the larger square 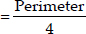
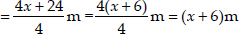
∴ Area of the smaller square = (side)2 = (x)2 m2
Area of the larger square = (x + 6)2 m2
According to the condition, x2 + (x + 6)2 = 468
⇒ x2 + x2 + 12x + 36 = 468
⇒ 2x2 + 12x - 432 = 0
⇒ x2 + 6x - 216 = 0 …(1)
Comparing (1) with ax2 + bx + c = 0, we get
∴ a = 1, b = 6, c = -216
∴ b2 - 4ac = (6)2 - 4(1)(-216) = 36 + 864 = 900
Since, 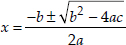
∴ 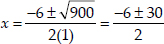
∴ Taking positive sign, we have 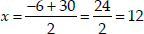
Taking negative sign, we get 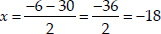
But the length of a square cannot be negative
∴ x = 12
⇒ length of the smaller square = 12 m
Thus, the length of the larger square
= x + 6 = 12 + 6 = 18 m
Find the nature of the roots of the following quadratic equations. If the real roots exist, find them :
(i) 2x2 - 3x + 5 = 0
(ii) 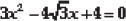
(iii) 2x2 - 6x + 3 = 0
Soln. : (i) Comparing the given quadratic equation with ax2 + bx + c = 0, we have
a = 2, b = -3, c = 5
∴ Discriminant = b2 - 4ac = (-3)2 - 4(2)(5)
= 9 - 40 = - 31 < 0
Since b2 - 4ac is negative
∴ The given quadratic equation has no real roots.
(ii) Comparing the given quadratic equation with ax2 + bx + c = 0, we get
a = 3, b = 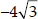 , c = 4
, c = 4
∴ 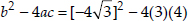 = (16 × 3) - 48
= (16 × 3) - 48
= 48 - 48 = 0
Thus, the given quadratic equation has two real roots which are equal. Hence, the roots are
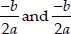
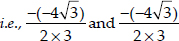
⇒ 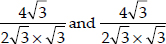
⇒ 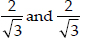
Thus, 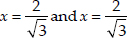
(iii) Comparing it with the general quadratic equation, we have
a = 2, b = -6, c = 3
∴ b2 - 4ac = (-6)2 - 4(2)(3)
= 36 - 24 = 12 > 0
∴ The given quadratic equation has two real and distinct roots, which are given by
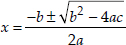
⇒ 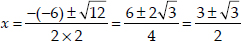
Thus, the roots are = 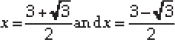
Find the values of k for each of the following quadratic equations so that they have two equal roots
(i) 2x2 + kx + 3 = 0
(ii) kx(x - 2) + 6 = 0
Soln. : (i) Comparing the given quadratic equation with ax2 + bx + c = 0, we get
a = 2, b = k, c = 3
∴ b2 - 4ac = (k)2 - 4(2)(3) = k2 - 24
∴ For a quadratic equation to have equal roots, b2 - 4ac = 0
∴ 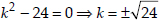 ⇒
⇒ 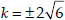
Thus, the required values of k are
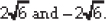
(ii) Comparing kx(x - 2) + 6 = 0
i.e., kx2 - 2kx + 6 = 0 with ax2 + bx + c = 0, we get
a = k, b = -2k, c = 6
∴ b2 - 4ac = (-2k)2 - 4(k)(6) = 4k2 - 24k
Since, the roots are real and equal,
∴ b2 - 4ac = 0 ⇒ 4k2 - 24k = 0
⇒ 4k(k - 6) = 0
⇒ 4k = 0 or k - 6 = 0
⇒ k = 0 or k = 6
But k cannot be 0, otherwise, the given equation is no more quadratic. Thus, the required value of k = 6.
Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 sq. metre ? If so, find its length and breadth.
SOLUTION:
Soln. : Let the breadth be x metres
∴ Length = 2x metres
Now, Area = Length × Breadth
= 2x × x metres2 = 2x2 sq.metre.
According to the given condition, 2x2 = 800
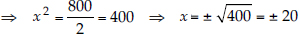
Therefore, x = 20 and x = -20
But x = -20 is not possible
[∴ breadth cannot be negative]
∴ x = 20 ⇒ 2x = 2 × 20 = 40
Thus, length = 40 m and breadth = 20 m
Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
SOLUTION:
Soln. : Let the age of one friend = x years
∴ The age of the other friend = (20 - x) years
[∴ Sum of their ages is 20 years]
Four years ago
Age of one friend = (x - 4) years
Age of other friend = (20 - x - 4) years
= (16 - x) years
According to the condition, (x - 4) × (16 - x) = 48
⇒ 16x - 64 - x2 + 4x = 48
⇒ - x2 + 20x - 64 - 48 = 0
⇒ - x2 + 20x - 112 = 0
⇒ x2 - 20x + 112 = 0 …(1)
Here, a = 1, b = - 20 and c = 112
∴ b2 - 4ac = (-20)2 - 4(1)(112)
= 400 - 448 = -48 < 0
Since b2 - 4ac is less than 0.
∴ The quadratic equation (1) has no real roots.
Thus, the given equation is not possible.
Is it possible to design a rectangular park of perimeter 80 m and area 400 m2? If so, find its length and breadth.
SOLUTION:
Soln. : Let the breadth of the rectangle be x m.
Since, the perimeter of the rectangle = 80 m.
∴ 2[Length + breadth] = 80
2[Length + x] = 80
⇒ 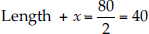
⇒ Length = (40 - x) m
∴ Area = (40 - x) × x sq.m = 40x - x2
Now, according to the given condition,
Area of the rectangle = 400 m2
∴ 40x - x2 = 400
⇒ - x2 + 40x - 400 = 0
⇒ x2 - 40x + 400 = 0 …(1)
Comparing (1) with ax2 + bx + c = 0, we get
a = 1, b = -40, c = 400
∴ b2 - 4ac = (-40)2 - 4(1)(400) = 1600 - 1600 = 0
Thus, the equation (1) has two equal and real roots.
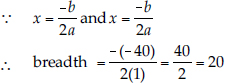
∴ Breadth, x = 20 m
∴ Length = (40 - x) = (40 - 20) m = 20 m.
Since Length = Breadth ∴ This rectangle is a square.