Circles - NCERT Questions
How many tangents can a circle have ?
SOLUTION:Soln. : A circle can have an infinite number of tangents.
Q 2.Fill in the blanks :
(i) A tangent to a circle intersects it in .......... point(s).
(ii) A line intersecting a circle in two points is called a ........... .
(iii) A circle can have .......... parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called ......... .
Soln. : (i) exactly one (ii) secant
(iii) two (iv) point of contact
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) 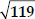 cm
cm
Soln. :(D) : In right ∆POQ,
OQ2 = OP2 + PQ2
⇒ 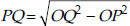

Draw a circle and two lines parallel to a given line such that one is a tangent and the other a secant to the circle.
SOLUTION:
Soln. : We have the required figure, as shown
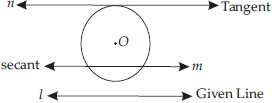
Here, l is the given line and a circle with centre O is drawn.
The line n is drawn which is parallel to l and tangent to the circle. Also, m is drawn parallel to line l and is a secant to the circle.
Choose the correct option:
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
Soln. : (A) ∵ QT is a tangent to the circle at T and OT is radius
∴ OT ┴ QT
Also, OQ = 25 cm
and QT = 24 cm
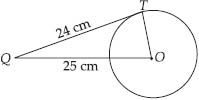
∴ Using Pythagoras theorem, we get
OQ2 = QT2 + OT2
⇒ OT2 = OQ2 - QT2 = 252 - 242 = 49
⇒ OT = 7
Thus, the required radius is 7 cm.
In figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(A) 60°
(B) 70°
(C) 80°
(D) 90°
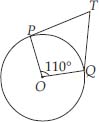
Soln. : (B) ∴ TQ and TP are tangents to a circle with centre O and ∠POQ = 110°
∴ OP ┴ PT and OQ ┴ QT
⇒ ∠OPT = 90° and ∠OQT = 90°
Now, in the quadrilateral TPOQ, we get
∴ ∠PTQ + 90° + 110° + 90° = 360°
[Angle sum property of a quadrilateral]
⇒ ∠PTQ + 290° = 360°
⇒ ∠PTQ = 360° - 290° = 70°
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Soln. : (A) : Since, O is the centre of the circle and two tangents from P to the circle are PA and PB.
∴ OA ┴ AP and OB ┴ BP
⇒ ∠OAP = ∠OBP = 90°
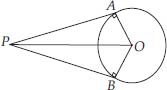
Now, in quadrilateral PAOB, we have :
∠APB + ∠PAO + ∠AOB + ∠PBO = 360°
⇒ 80° + 90° + ∠AOB + 90° = 360°
⇒ 260° + ∠AOB = 360°
⇒ ∠AOB = 360° - 260° ⇒ ∠AOB = 100°
In right ∆OAP and right ∆OBP, we have
OP = OP [Common]
∠OAP = ∠OBP [Each = 90°]
OA = OB [Radii of the same circle]
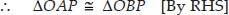
⇒ ∠POA = ∠POB [By CPCT]
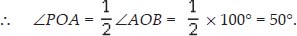
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
SOLUTION:
Soln. : In the figure, PQ is diameter of the given circle and O is its centre.
Let tangents AB and CD be drawn at the end points of the diameter PQ.
Since the tangents at a point to a circle is perpen-dicular to the radius through the point.
∴ PQ ┴ AB
⇒ ∠APQ = 90°
And PQ ┴ CD
⇒ ∠PQD = 90°
⇒ ∠APQ = ∠PQD
But they form a pair of alternate angles.
∴ AB || CD.
Hence the two tangents are parallel.
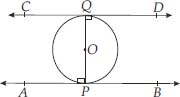
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
SOLUTION:
Soln. : In the figure, the centre of the circle is O and tangent AB touches the circle at P. If possible, let PQ be perpendicular to AB such that it is not passing through O.
Join OP.
Since tangent at a point to a circle is perpendicular to the radius through that point,
∴ OP ┴ AB
⇒ ∠OPB = 90° ...(1)
But by construction,
PQ ┴ AB
⇒ ∠QPB = 90° ...(2)
From (1) and (2),
∠QPB = ∠OPB
which is possible only when O and Q coincide. Thus, the perpendicular at the point of contact to the tangent to a circle passes through the centre.
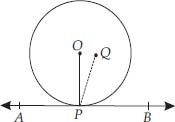
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
SOLUTION:
Soln. : ∵ The tangent to a circle is perpendicular to the radius through the point of contact.
∴ ∠OTA = 90°
Now, in the right ∆OTA, we have:
OA2 = OT2 + AT2 [Pythagoras theorem]
⇒ 52 = OT2 + 42
⇒ OT2 = 52 - 42
⇒ OT2 = (5 - 4)(5 + 4)
⇒ OT2 = 1 × 9
= 9 = 32
⇒ OT = 3
Thus, the radius of the circle is 3 cm.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
SOLUTION:
Soln. : In the figure, O is the common centre, of the given concentric circles.
AB is a chord of the bigger circle such that it is a tangent to the smaller circle at P.
Since OP is the radius of the smaller circle. ∴ OP ┴ AB ⇒ ∠APO = 90°
Also, radius perpendicular to a chord bisects the chord.
∴ OP bisects AB
⇒ 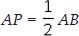
Now, in right ∆APO,
OA2 = AP2 + OP2
⇒ 52 = AP2 + 32 ⇒ AP2 = 52 - 32
⇒ AP2 = 42 ⇒ AP = 4 cm
⇒ 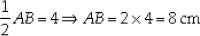
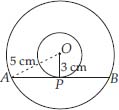
Hence, the required length of the chord AB is 8 cm.
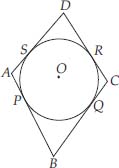
A quadrilateral ABCD is drawn to circumscribe a circle (see figure).
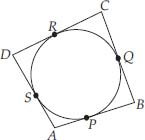
Prove that AB + CD = AD + BC
Soln. : Since the sides of quadrilateral ABCD, i.e., AB, BC, CD and DA touch the circle at P, Q, R and S respectively, and the lengths of two tangents to a circle from an external point are equal.
∴ AP = AS
BP = BQ
DR = DS and CR = CQ
Adding them, we get
(AP + BP) + (CR + RD) = (BQ + QC) + (DS + SA)
⇒ AP + CD = BC + DA
In the figure, XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X'Y' at B.
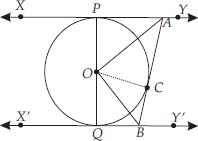
Prove that ∠AOB = 90°.
Soln. : ∵ The tangents drawn to a circle from an external point are equal.
∴ AP = AC, Join OC
In ∆PAO and ∆CAO, we have :
AO = AO [Common]
OP = OC [Radii of the same circle]
AP = AC [Proved above]
⇒ 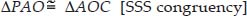
∴ ∠PAO = 2∠CAO
⇒ ∠PAC = 2∠CAO ...(1)
Similarly ∠CBQ = 2∠CBO ...(2)
Again, we know that sum of internal angles on the same side of a transversal is 180°.
∴ ∠PAC + ∠CBQ = 180°
⇒ 2∠CAO + 2∠CBO = 180°
[From (1) and (2)]
⇒ 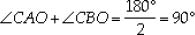 ...(3)
...(3)
Also in ∆AOB, ∠BAO + ∠ABO + ∠AOB = 180°
[Sum of angles of a triangle]
⇒ ∠CAO + ∠CBO + ∠AOB = 180° [By (3)]
⇒ 90° + ∠AOB = 180°
⇒ ∠AOB = 180° - 90°
⇒ ∠AOB = 90°.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
SOLUTION:
Soln. : Let PA and PB be two tangents drawn from an external point P to a circle with centre O.
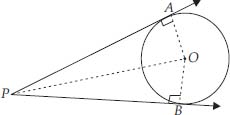
Now, in right ∆OAP and right ∆OBP, we have
PA = PB [Tangents to circle from an
external point]
OA = OB [Radii of the same circle]
OP = OP [Common]
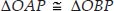 [By SSS congruency]
[By SSS congruency]
∴ ∠OPA = ∠OPB [By C.P.C.T.]
and ∠AOP = ∠BOP
⇒ ∠APB = 2∠OPA and ∠AOB = 2∠AOP
But ∠AOP = 90° - ∠OPA
⇒ 2∠AOP = 180° - 2∠OPA
⇒ ∠AOB = 180° - ∠APB
⇒ ∠AOB + ∠APB = 180°. (Proved)
Prove that the parallelogram circumscribing a circle is a rhombus.
SOLUTION:
Soln. : We have ABCD, a parallelogram which circumscribes a circle (i.e., its sides touch the circle) with centre O.
Since tangents to a circle from an external point are equal in length,
∴ AP = AS
BP = BQ
CR = CQ
DR = DS
Adding, we get
(AP + BP) + (CR + DR)
= (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
But AB = CD [opposite sides of parallelogram]
and BC = AD
∴ AB + CD = AD + BC ⇒ 2AB = 2BC
⇒ AB = BC
Similarly AB = DA and DA = CD
Thus, AB = BC = CD = AD
Hence ABCD is a rhombus.
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.
SOLUTION:
Soln. : Here ∆ABC circumscribe the circle with centre O. Also, radius = 4 cm
∵ The sides BC, CA and AB touch the circle at D, E and F respectively.
∴ BF = BD = 8 cm
CD = CE = 6 cm
AF = AE = x cm (say)
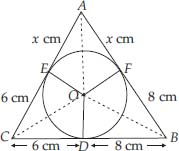
⇒ The sides of the triangle are :
14 cm, (x + 6) cm and (x + 8) cm Perimeter of ∆ABC
= [14 + (x + 6) + (x + 8)] cm
= [14 + 6 + 8 + 2x] cm
= 28 + 2x cm
⇒ Semi perimeter of ∆ABC
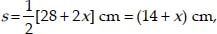
where a = AB, b = BC, c = AC
∴ s - a = (14 + x) - (8 + x) = 6
s - b = (14 + x) - (14) = x
s - c = (14 + x) - (16 + x) = 8
∴ Area of ∆ABC = 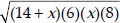 cm2
cm2
= 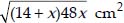 ...(1)
...(1)
Now, ar(∆OBC) = 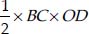
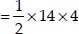 = 28 cm2 [∵ OD = Radius]
= 28 cm2 [∵ OD = Radius]
ar (∆OCA) 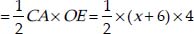
= (2x + 12) cm2
ar (∆OAB) 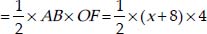
= (2x + 16) cm2
∴ ar (∆ABC) = ar (∆OBC) + ar (∆OCA) + ar (∆OAB)
= 28 cm2 + (2x + 12) cm2 + (2x + 16) cm2
= (28 + 12 + 16) + 4x cm2
= (56 + 4x) cm2 ...(2)
From (1) and (2), we have
56 + 4x = 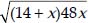
⇒ 4[14 + x] = 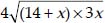
⇒ 14 + x = 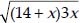
Squaring both sides (14 + x)2 = (14 + x)3x
⇒ 196 + x2 + 28x = 42x + 3x2
⇒ 2x2 + 14x - 196 = 0
⇒ x2 + 7x - 98 = 0
⇒ (x - 7) (x + 14) = 0
⇒ x - 7 = 0
⇒ x = 7 or x + 14 = 0
⇒ x = -14
But x = -14 is rejected.
∴ x = 7 cm
Thus, AB = 8 + 7 = 15 cm
BC = 8 + 6 = 14 cm
CA = 6 + 7 = 13 cm.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
SOLUTION:
Soln. : We have a circle with centre O. A quadrilateral ABCD is such that the sides AB, BC, CD and DA touch the circle at P, Q, R and S respectively.
Let us join OP, OQ, OR and OS.
We know that two tangents drawn from an external point to a circle subtend equal angles at the centre.
∴ ∠1 = ∠2
∠3 = ∠4
∠5 = ∠6
and ∠7 = ∠8
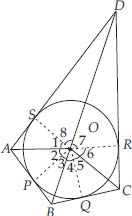
Also, the sum of all the angles around a point is 360°.
∴ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8
= 360°
∴ 2[∠1 + ∠8 + ∠5 + ∠4] = 360°
⇒ (∠1 + ∠8 + ∠5 + ∠4) = 180° ...(1)
And 2[∠2 + ∠3 + ∠6 + ∠7] = 360°
⇒ (∠2 + ∠3) + (∠6 + ∠7) = 180° ...(2)
Since, ∠2 + ∠3 = ∠AOB, ∠6 + ∠7 = ∠COD
∠1 + ∠8 = ∠AOD, ∠4 + ∠5 = ∠BOC
∴ From (1) and (2), we have:
∠AOD + ∠BOC = 180°
and ∠AOB + ∠COD = 180°(Proved)